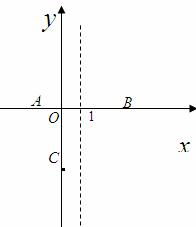
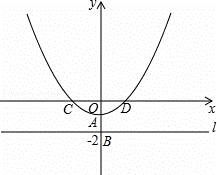
如图，在平面直角坐标系xOy中，直线l⊥y轴于点B（0，﹣2），A为OB的中点，以A为顶点的抛物线y=ax2+c与x轴交于C、D两点，且CD=4，点P为抛物线上的一个动点，以P为圆心，PO为半径画圆．
（1）求抛物线的解析式；
（2）若⊙P与y轴的另一交点为E，且OE=2，求点P的坐标；
（3）判断直线l与⊙P的位置关系，并说明理由．
答案
解：（1）∵点A为OB的中点，
∴点A的坐标为（0，﹣1）．
∵CD=4，由抛物线的对称性可知：点C（﹣2，0），D（2，0），
将点A（0，﹣1），C（﹣2，0），D（2，0）代入抛物线的解析式得：
，
解得：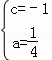
，
∴抛物线得解析式为y=
．
（2）如下图：过点P1作P1F⊥OE．
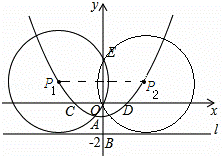
∵OE=2，
∴点E的坐标为（0，2）．
∵P1F⊥OE．
∴EF=OF．
∴点P1的纵坐标为1．
同理点P2的纵坐标为1．
将y=1代入抛物线的解析式得：x1=
，x2=2
．
∴点P1（﹣2，1），P2（﹣2，1）．
如下图：
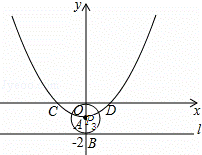
当点E与点B重合时，点P3与点A重合，
∴点P3的坐标为（0，﹣1）．
综上所述点P的坐标为（﹣2
，1）或（2，1）或（0，﹣1）．
（3）设点P的坐标为（m，
），
∴圆的半径OP=
=
，
点P到直线l的距离=
﹣（﹣2）=
+1．
∴d=r．
∴直线l与圆P相切．
