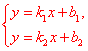函数:一般地,在一个变化过程中,如果有两个自变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。
如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值。
变量:
在一个变化过程中,我们称数值发生变化的量为变量。(数学中,常常为x,而y则随x值的变化而变化),有些数值是不随变量而改变的,我们称它们为常量。
自变量:函数一个与它量有关联的变量,这一量中的任何一值都能在它量中找到对应的固定值。
因变量(函数):随着自变量的变化而变化,且自变量取唯一值时,因变量(函数)有且只有唯一值与其相对应。
1、变量:在一个变化过程中,我们称数值发生变化的量为变量。
2、函数:一般地,在一个变化过程中,如果有两个自变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。
如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值。
变量的关系:
在具体情境中,感受两个变量之间的关系,就是一个变量随着另一个变量的变化情况,例如随着一个变量的变化,有的变量是呈匀速变化的,有的变量是呈不匀速变化的;
进而发现实际情景中的变量及其相互关系,并确定其中的自变量和因变量,会用运动变化的基本观点观察事物。也就是说,在两个有相依关系的变量中,其中一个是自变量,另一个是因变量;
自变量和因变量之间的变化关系可以用表格来刻画,也可以用图象来描述,并能对未来的趋势加以预测。
函数自变量的取值范围的确定:
使函数有意义的自变量的取值的全体,叫做函数自变量的取值范围.
自变量的取值范围的确定方法:
首先要考虑自变量的取值必须使解析式有意义,
①当解析式为整式时,自变量的取值范围是全体实数;
②当解析式是分数的形式时,自变量的取值范围是使分母不为零的所有实数;
③当解析式中含有平方根时,自变量的取值范围是使被开方数不小于零的实数;
④当函数解析式表示实际问题时,自变量的取值必须使实际问题有意义。
1、通过探索具体问题中的数量关系和变化规律来了解常量、变量的意义;
2、学会用含一个变量的代数式表示另一个变量;
3、结合实例,理解函数的概念以及自变量的意义;在理解掌握函数概念的基础上,确定函数关系式;
4、会根据函数解析式和实际意义确定自变量的取值范围。
能力要求:知道
课时要求:40
考试频率:选考
分值比重:2
![]() 解析式
解析式![]() x
x ![]() 横
横 ![]() 正
正 ![]() 负
负 ![]()