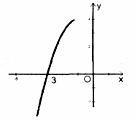
某水果店销售某中水果,由历年市场行情可知,从第1月至第12月,这种水果每千克售价y1(元)与销售时间第x月之间存在如图1(一条线段)的变化趋势,每千克成本y2(元)与销售时间第x月满足函数关系式y2=mx2﹣8mx+n,其变化趋势如图2.
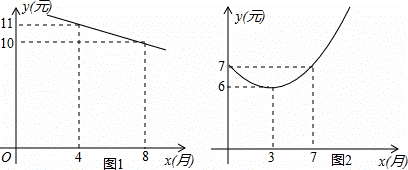
(1)求y2的解析式;
(2)第几月销售这种水果,每千克所获得利润最大?最大利润是多少?
答案
解:(1)由图可知,y2=mx2﹣8mx+n经过点(3,6),(7,7),
∴![]() ,
,
解得![]() .
.
∴y2=x2﹣x+![]() (1≤x≤12);
(1≤x≤12);
(2)设y1=kx+b(k≠0),
由图可知,函数图象经过点(4,11),(8,10),
则![]() ,
,
解得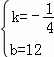 ,
,
所以,y1=﹣x+12,
所以,每千克所获得利润=(﹣x+12)﹣(x2﹣x+![]() )
)
=﹣x+12﹣x2+x﹣![]()
=﹣x2+x+![]()
=﹣(x2﹣6x+9)++![]()
=﹣(x﹣3)2+![]() ,
,
∵﹣<0,
∴当x=3时,所获得利润最大,为![]() 元.
元.
答:第3月销售这种水果,每千克所获得利润最大,最大利润是![]() 元/千克.
元/千克.

 方程有两个不等实数根;
方程有两个不等实数根; 方程有两个相等实数根;
方程有两个相等实数根; 方程没有实数根。
方程没有实数根。 △>0;
△>0; △=0;
△=0; △<0。
△<0。 (△>0)与x轴两交点间的距离的问题。
(△>0)与x轴两交点间的距离的问题。