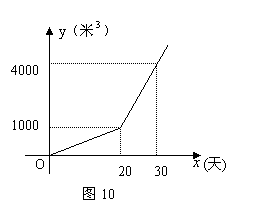
如图,某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.
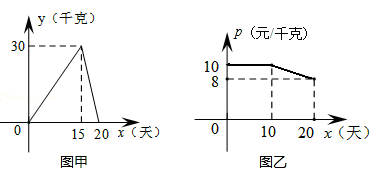
(1)直接写出y与x之间的函数关系式;
(2)分别求出第10天和第15天的销售金额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
答案
解:(1)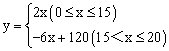 。
。
(2)∵第10天和第15天在第10天和第20天之间,
∴当10≤x≤20时,设销售单价p(元/千克)与销售时间x(天)之间的函数解析式为p=mx+n,
∵点(10,10),(20,8)在z=mx+n的图象上,
∴![]() ,解得:
,解得: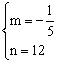 。
。
∴![]() 。
。
当x=10时,![]() ,y=2×10=20,销售金额为:10×20=200(元);
,y=2×10=20,销售金额为:10×20=200(元);
当x=15时,![]() ,y=2×15=30,销售金额为:9×30=270(元)。
,y=2×15=30,销售金额为:9×30=270(元)。
故第10天和第15天的销售金额分别为200元,270元。
(3)若日销售量不低于24千克,则y≥24。
当0≤x≤15时,y=2x,
解不等式2x≥24,得x≥12;
当15<x≤20时,y=﹣6x+120,
解不等式﹣6x+120≥24,得x≤16。
∴12≤x≤16。
∴“最佳销售期”共有:16﹣12+1=5(天)。
∵![]() (10≤x≤20)中
(10≤x≤20)中![]() <0,∴p随x的增大而减小。
<0,∴p随x的增大而减小。
∴当12≤x≤16时,x取12时,p有最大值,此时![]() =9.6(元/千克)。
=9.6(元/千克)。
故此次销售过程中“最佳销售期”共有5天,在此期间销售单价最高为9.6元
【解析】
试题分析:(1)分两种情况进行讨论:①0≤x≤15;②15<x≤20,针对每一种情况,都可以先设出函数的解析式,再将已知点的坐标代入,利用待定系数法求解:
①当0≤x≤15时,设日销售量y与销售时间x的函数解析式为y=k1x,
∵直线y=k1x过点(15,30),∴15k1=30,解得k1=2。
∴y=2x(0≤x≤15);
②当15<x≤20时,设日销售量y与销售时间x的函数解析式为y=k2x+b,
∵点(15,30),(20,0)在y=k2x+b的图象上,
∴![]() ,解得:
,解得:![]() 。
。
∴y=﹣6x+120(15<x≤20)。
综上所述,可知y与x之间的函数关系式为: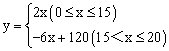 。
。
(2)日销售金额=日销售单价×日销售量.由于第10天和第15天在第10天和第20天之间,当10≤x≤20时,设销售单价p(元/千克)与销售时间x(天)之间的函数关系式为p=mx+n,由点(10,10),(20,8)在p=mx+n的图象上,利用待定系数法求得p与x的函数解析式,继而求得10天与第15天的销售金额。
(3)日销售量不低于24千克,即y≥24.先解不等式2x≥24,得x≥12,再解不等式﹣6x+120≥24,得x≤16,则求出“最佳销售期”共有5天;然后根据![]() (10≤x≤20),利用一次函数的性质,即可求出在此期间销售时单价的最高值。
(10≤x≤20),利用一次函数的性质,即可求出在此期间销售时单价的最高值。