2.6 实数 ( 2 )

教学目标：

( 一 ) 教学知识点

1. 了解有理数的运算法则在实数范围内仍然适用

2. 用类比的方法，引入实数的运算法则、运算律，并能用这些法则，运算律在实数范围内正确计算

3. 正确运用公式

.

( 二 ) 能力训练要求

1. 让学生根据现有的条件或式子找出它们的共性，进而发现规律，培养学生的钻研精神和创新能力

2. 能用类比的方法去解决问题，找规律，用旧知识去探索新知识

( 三 ) 情感与价值观要求

通过探索规律的过程，培养学生学习的主动性，敢于探索，大胆猜想，和同学积极交流，增强学习数学的兴趣和信心。

教学重点：

1. 用类比的方法，引入实数的运算法则、运算律，并能在实数范围内正确进行运算 .

2. 发现规律：

，并能用规律进行计算

教学难点：

1. 类比的学习方法 .

2. 发现规律的过程 .

教学方法：

类比法 .

教学过程：

Ⅰ . 新课导入

上节课我们学习了实数的定义、实数的两种分类，还有在实数范围内如何求相反数、倒数、绝对值，它们的求法和在有理数范围内的求法相同 . 那么在有理数范围内的运算法则、运算律等能不能在实数范围内继续用呢？本节课让我们来一起进行探究 .

Ⅱ . 新课讲解

1. 有理数的运算法则在实数范围内仍然适用 .

［师］大家先回忆一下我们在有理数范围内学过哪些法则和运算律 .

［生］加、减、乘、除运算法则，加法交换律，结合律，分配律 .

［师］好 . 下面我们就来验证一下这些法则和运算律是否在实数范围内适用 . 我们知道实数包括有理数和无理数，而有理数不用再考虑，只要对无理数进行验证就可以了 .

如： ，

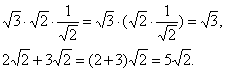
所以说明有理数的运算法则与运算律对实数仍然适用 . 下面看一些例题 . 计算：

(1) ； (2) ； (3)(2 ) ² ； (4) .

2. 做一做

填空：

(1) =_________ ， =_________ ；

(2) =_________ ， =_________ ；

(3) =_________ ， =_________ ；

(4) _________ ， =_________.

［师］通过上面计算的结果，大家认真总结找出规律 . 如果把具体的数字换成字母应怎样表示呢？

( a ≥ 0, b ≥ 0) ；

( a ≥ 0, b ＞ 0)

并作一些练习 . 化简：

(1) ； (2) － 4 ； (3)( － 1) ² ； (4) ； (5) .

3. 例题讲解

［例题］化简：

(1) ； (2) ； (3)( +1) ² ； (4) .

Ⅲ . 课堂练习

( 一 ) 随堂练习

化简： (1) ； (2) ； (3)(1+ )(2 － ) ； (4)( ) ² .

( 二 ) 补充练习

1. 化简：

(1) ； (2)(1+ )( － 2) ； (3) ； (4) ；

(5) ； (6)

Ⅳ . 课时小结

本节课主要掌握以下内容 .

1. 在实数范围内，有理数的运算法则、运算律仍然适用，并能正确运用 .

2. ( a ≥ 0, b ≥ 0) ； ( a ≥ 0, b ＞ 0) 的推导及运用 .

Ⅴ . 课后作业

习题 2.9

1. 化简：

(1) ； (2) ； (3) ； (4) － 21.

Ⅵ . 活动与探究

下面的每个式子各等于什么数？

.

由此能得到一般的规律吗？

对于一个实数 a 、 一定等于 a 吗？

当 a ≥ 0 时， = a .

当 a ＜ 0 时，有

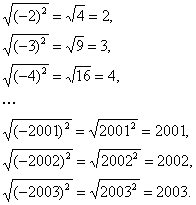
所以当 a ＜ 0 时，有 = － a .

板书设计：

教学反思：这节内容是两个公式的推导与运用。当然计算的熟练始终是初中阶段的一个大的环节，只有让学生多做练习才能熟练。有待另外花时间加大训练。

摘自 http://www.12999.com/index.html