初中数学23．1圆的认识教案

当前位置：

学科首页

初中数学教案

初中数学23．1圆的认识教案

教案

初中数学

3次下载

纠错

立即下载

从不同方向看

教案示例

23.1.1 圆的基本元素

教学目标：使学生理解圆、等圆、等弧、圆心角等概念，让学生深刻认识圆中的基本概念。

重点难点：

1 、重点：圆中的基本概念的认识。

2 、难点：对等弧概念的理解。

教学过程：

一、圆是如何形成的？

请同学们画一个圆，并从画圆的过程中阐述圆是如何形成的。

如右图，线段 OA 绕着它固定的一个端点 O 旋转一周，另一个端点 A 随之旋转所形成的图形。同学们想一想，如何在操场上画出一个很大的圆？说说你的方法。

由以上的画圆和解答问题的过程中，让同学们思考圆的位置是由什么决定的？而大小又是由谁决定的？（圆的位置由圆心决定，圆的大小由半径长度决定）

二、圆的基本元素

问题：据统计，某学校的同学上学方式是， 50% 的同学步行上学， 20% 的同学坐公共汽车上学，其他方式上学的同学有 30% ，请你用扇形统计图反映这个学校学生的上学方式。

我们是用圆规画出一个圆，再将圆划分成一个个扇形，图 23.1.1 就是反映学校学生上学方式的扇子形统计图。

如图 23.1.2 ，线段 OA 、 OB 、 OC 都是圆的半径，线段 AB 为直径， . 这个以点 O 为圆心的圆叫作 “圆 O ”，记为“⊙ O ”。线段 AB 、 BC 、 AC 都是圆 O 中的弦，曲线 BC 、 BAC 都是圆中的弧，分别记为、，其中像弧这样小于半圆周的圆弧叫做劣弧，像弧这样的大于半圆周的圆弧叫做优弧。∠ AOB 、∠ AOC 、∠ BOC 就是圆心角

结合上面的扇形统计图，进一步阐述圆心角、优弧、劣弧等圆中的基本元素。

三、典型例题

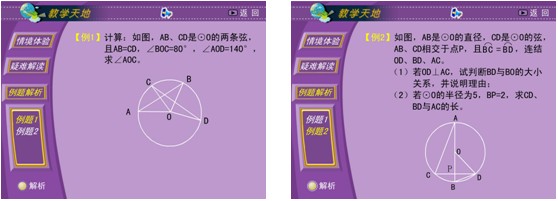
四、小结本节课我们认识了圆中的一些元素，同学应能从具体的图形中对这些元素加以识别。

五、作业

1 、如图， AB 是⊙ O 的直径， C 点在⊙ O 上，那么，哪一段弧是优弧，哪一段弧是劣弧？

2 、经过 A 、 B 两点的圆的几个？它们的圆心都在哪里？

3 、长方形的四个顶点在以为圆心，以为半径的圆上。

4 、如图，已知 AB 是⊙ O 的直径， AC 为弦， OD ∥ BC ，交 AC 于 D ，，求 OD 的长。

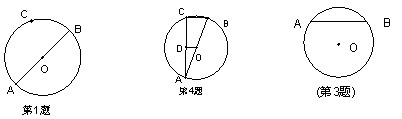
5 、已知：如图， OA 、 OB 为⊙ O 的半径， C 、 D 分别为 OA 、 OB 的中点，试说明 AD=BC 。

23.1.2 圆的对称性

教学目标：

使学生知道圆是中心对称图形和轴对称图形 , 并能运用其特有的性质推出在同一个圆中 , 圆心角、弧、弦之间的关系，能运用这些关系解决问题，培养学生善于从实验中获取知识的科学的方法。

重点难点：

1 、重点：由实验得到同一个圆中，圆心角、弧、弦三者之间的关系。

2 、难点：运用同一个圆中，圆心角、弧、弦三者之间的关系解决问题。

教学过程：

一、由问题引入新课：要同学们画两个等圆，并把其中一个圆剪下，让两个圆的圆心重合，使得其中一个圆绕着圆心旋转，可以发现，两个圆都是互相重合的。如果沿着任意一条直径所在的直线折叠，圆在这条直线两旁的部分会完全重合。

由以上实验，同学们发现圆是中心对称图形吗？对称中心是哪一点？圆不仅是中心对称圆形，而且还是轴对称图形，过圆心的每一条直线都是圆的对称轴。

二、新课

1 、同一个圆中，相等的圆心角所对的弧相等、所对的弦相等。

垂直于弦的直径平分弦，并且平分弦所对的两条弧。 ( 垂径定理 )

实验 1 、将图形 23.1.3 中的扇形 AOB 绕点 O 逆时针旋转某个角度，得到图 23.1.4 中的图形，同学们可以通过比较前后两个图形，发现∠ AOB = ∠ AOB ， AB = AB ，

。

实质上，∠ AOB 确定了扇形 AOB 的大小，所以，在同一个圆中，如果圆心角相等，那么它所对的弧相等，所对的弦相等。

问题：在同一个圆中，如果弧相等，那么所对的圆心角，所对的弦是否相等呢？

在同一个圆中，如果弦相等，那么所对的圆心角，所对的弧是否相等呢？

实验 2 、如图 23.1.7 ，如果在图形纸片上任意画一条垂直于直径 CD 的弦 AB ，垂足为 P ，再将纸片沿着直径 CD 对折，比较 AP 与 PB 、与，你能发现什么结论？

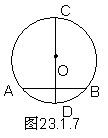
显然，如果 CD 是直径， AB 是⊙ O 中垂直于直径的弦，那么 AP = BP ， = ，。请同学们用一句话加以概括。

垂直于弦的直径平分弦，并且平分弦所对的两条弧

2 、同一个圆中，圆心角、弧、弦之间的关系的应用。

（ 1 ）思考：如图，在一个半径为 6 米的圆形花坛里，准备种植六种不同颜色的花卉，要求每种花卉的种植面积相等，请你帮助设计种植方案。

（ 2 ）如图 23.1.5 ，在⊙ O 中， AC = BC ，∠ 1 = 45 º ，求∠ 2 的度数。

三、课堂小结

本节课我们通过实验得到了圆不仅是中心对称图形，而且还是轴对称图形，而由圆的对称性又得出许多圆的许多性质，即（ 1 ）同一个圆中，相等的圆心角所对弧相等，所对的弦相等。（ 2 ）在同一个圆中，如果弧相等，那么所对的圆心角，所对的弦相等。（ 3 ）在同一个圆中，如果弦相等，那么所对的圆心角，所对的弧相等。（ 4 ）垂直于弦的直径平分弦，并且平分弦所对的两条弧。

四、作业

习题 1 、 2 、 3 、 4 、 5

23.1.3 圆周角

教学目标：

使学生知道什么样的角是圆周角，了解圆周角和圆心角的关系，直径所对的圆周角的特征；并能应用圆心角和圆周角的关系、直径所对的圆周角的特征解决相关问题，同时，通过对圆心角和圆周角关系的探索，培养学生运用已有知识，进行实验、猜想、论证，从而得到新知。

重点难点：

1 、重点：认识圆周角，同一条弧的圆周角和圆心角的关系，直径所对的圆周角的特征。

2 、难点：发现同一条弧的圆周角和圆心角的关系，利用这个关系进一步得到其他知识，运用所得到的知识解决问题。

教学过程：

一、认识圆周角

如下图，同学们能找到圆心角吗？它具有什么样的特征？（顶点在圆心，两边与圆相交的角叫做圆心角），今天我们要学习圆中的另一种特殊的角，它的名称叫做圆周角。

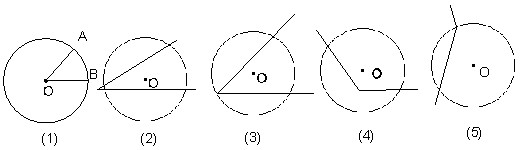
究竟什么样的角是圆周角呢？像图（ 3 ）中的解就叫做圆周角，而图（ 2 ）、（ 4 ）、（ 5 ）中的角都不是圆周角。同学们可以通过讨论归纳如何判断一个角是不是圆周角。（顶点在圆上，两边与圆相交的角叫做圆周角）

练习：试找出图中所有相等的圆周角。

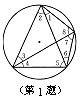
二、圆周角的度数

探究半圆或直径所对的圆周角等于多少度？而的圆周角所对的弦是否是直径？

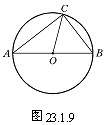
如图 23.1.9 ，线段 AB 是⊙ O 的直径，点 C 是⊙ O 上任意一点（除点 A 、 B ），那么，∠ ACB 就是直径 AB 所对的圆周角 . 想想看，∠ ACB 会是怎么样的角？为什么呢？

启发学生用量角器量出的度数，而后让同学们再画几个直径 AB 所对的圆周角，并测量出它们的度数，通过测量，同学们感性认识到直径所对的圆周角等于 90º ( 或直角 ) ，进而给出严谨的说明。

证明：因为 OA ＝ OB ＝ OC ，所以△ AOC 、△ BOC 都是等腰三角形，所以∠ OAC ＝∠ OCA ，∠ OBC ＝∠ OCB ；又∠ OAC ＋∠ OBC ＋∠ ACB ＝ 180 °，所以∠ ACB ＝∠ OCA ＋∠ OCB ＝＝ 90 º ；因此，不管点 C 在⊙ O 上何处（除点 A 、 B ），∠ ACB 总等于 90 °，即

半圆或直径所对的圆周角都相等，都等于 90º （直角）。反过来也是成立的，即 90º 的圆周角所对的弦是圆的直径

三、探究同一条弧所对的圆周角和圆心角的关系

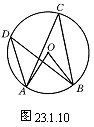
1 、分别量一量图 23.1.10 中弧 AB 所对的两个圆周角的度数比较一下；再变动点 C 在圆周上的位置，看看圆周角的度数有没有变化；你发现其中有什么规律吗？

2 、分别量出图 23.1.10 中弧 AB 所对的圆周角和圆心角的度数，比较一下，你发现什么？

我们可以发现，圆周角的度数没有变化，并且圆周角的度数恰好为同弧所对的圆心角的度数的一半。

由上述操作可以猜想：在一个圆中，一条弧所对的任意一个圆周角的大小都等于该弧所对的圆心角的一半。

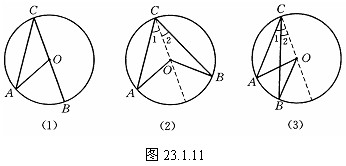
为了验证这个猜想，如图 23.1.11 所示，可将圆对折，使折痕经过圆心 O 和圆周角的顶点 C ，这时可能出现三种情况：（ 1 ）折痕是圆周角的一条边，（ 2 ）折痕在圆周角的内部，（ 3 ）折痕在圆周角的外部。

我们来分析一下第一种情况：如图 23.1.11 （ 1 ），由于 OA ＝ OC ，因此∠ A ＝∠ C ，

而∠ AOB 是△ OAC 的外角，所以∠ C ＝ ∠ AOB .

对（ 2 ）、（ 3 ），有同样的结论 . （让同学们把推导的过程写出来），由以上的猜想和推导可以得到：一条弧所对的圆周角等于该弧所对的圆心角的一半。

思考：

1 、在同一个圆中，同弧或等弧所对的圆周角相等吗？为什么？相等的圆周角所对的弧相等吗，为什么？

2 、你能找出左图中相等的圆周角吗？

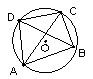
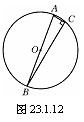
3 、右图是一个圆形的零件，你能告诉我，它的圆心的位置吗？你有什么简捷的办法？

4 、如图，如图 23.1.12 ， AB 是⊙ O 的直径，∠ A ＝ 80 ° ．求∠ ABC 的度数．

四、典型例题

五、小结

本节课我们一同探究了同圆或等圆中，一条弧所对的圆周角等于这条弧所对的圆心角的一半；由这个结论进一步得到：同圆或等圆中，同弧或等弧所对的圆周角相等，都等于该弧所对的圆心角的一半；相等的圆周角所对的弧相等；半圆或直径所对的圆周角都相等，都等于 90 ° （直角）。 90 ° （直角）的圆周角所对的弦是圆的直径等结论，希望同学们通过复习，记住这些知识，并能做到灵活应用他们解决相关问题。