在直角坐标系中,我们将圆心坐标和半径均为整数的圆称为“整圆”.如图所示,直线l:y=kx+4![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为“整圆”的点P个数是_____个.
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为“整圆”的点P个数是_____个.
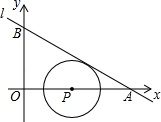
6.
【分析】
根据直线的解析式求得OB=4![]() ,进而求得OA=12,根据切线的性质求得PM⊥AB,根据∠OAB=30°,求得PM=
,进而求得OA=12,根据切线的性质求得PM⊥AB,根据∠OAB=30°,求得PM=![]() PA,然后根据“整圆”的定义,即可求得使得⊙P成为整圆的点P的坐标,从而求得点P个数.
PA,然后根据“整圆”的定义,即可求得使得⊙P成为整圆的点P的坐标,从而求得点P个数.
【详解】
∵直线l:y=kx+4![]() 与x轴、y轴分别交于A、B,
与x轴、y轴分别交于A、B,
∴B(0,4![]() ),
),
∴OB=4![]() ,
,
在Rt△AOB中,∠OAB=30°,
∴OA=![]() OB=
OB=![]() ×4
×4![]() =12,
=12,
∵⊙P与l相切,设切点为M,连接PM,则PM⊥AB,

∴PM=![]() PA,
PA,
设P(x,0),
∴PA=12﹣x,
∴⊙P的半径PM=![]() PA=6﹣
PA=6﹣![]() x,
x,
∵x为整数,PM为整数,
∴x可以取0,2,4,6,8,10,6个数,
∴使得⊙P成为整圆的点P个数是6.
故答案是:6.
【点睛】
本题考查动点问题,需要用到圆的切线,一次函数的知识点,解题关键是得出PM=![]() PA=6﹣
PA=6﹣![]() x.
x.
如图,直线AB与CD相交于点O,OA=4cm,∠AOC=30°,且点A也在半径为1cm的⊙P上,点P在直线AB上,⊙P以1cm/s的速度从点A出发向点B的方向运动_________s时与直线CD相切.
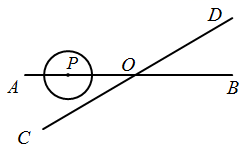
1或5
【分析】
分类讨论:当点P在射线OA上时,过点P作PE⊥AB于点E,根据切线的性质得到PE=1cm,利用30度角所对的直角边等于斜边一半的性质的OP=2PE=2cm,求出⊙P移动的距离为4-2-1=1cm,由此得到⊙P运动时间;当点P在射线OB上时,过点P作PF⊥AB于点F,同样方法求出运动时间.
【详解】
当点P在射线OA上时,如图,过点P作PE⊥AB于点E,则PE=1cm,
∵∠AOC=30°,
∴OP=2PE=2cm,
∴⊙P移动的距离为4-2-1=1cm,
∴运动时间为![]() s;
s;
当点P在射线OB上时,如图,过点P作PF⊥AB于点F,则PF=1cm,
∵∠AOC=30°,
∴OP=2PF=2cm,
∴⊙P移动的距离为4+2-1=5cm,
∴运动时间为![]() s;
s;
故答案为:1或5.

【点睛】
此题考查动圆问题,圆的切线的性质定理,含30度角的直角边等于斜边一半的性质,解题中注意运用分类讨论的思想解答问题.
如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() 为平面内的动点,且满足
为平面内的动点,且满足![]() ,
,![]() 为直线
为直线![]() 上的动点,则线段
上的动点,则线段![]() 长的最小值为________.
长的最小值为________.

![]()
【分析】
由直径所对的圆周角为直角可知,动点![]() 轨迹为以
轨迹为以![]() 中点
中点![]() 为圆心,
为圆心,![]() 长为直径的圆,求得圆心
长为直径的圆,求得圆心![]() 到直线的距离,即可求得答案.
到直线的距离,即可求得答案.
【详解】
∵![]() ,
,
∴动点![]() 轨迹为:以
轨迹为:以![]() 中点
中点![]() 为圆心,
为圆心,![]() 长为直径的圆,
长为直径的圆,
∵![]() ,
,![]() ,
,
∴点M的坐标为:![]() ,半径为1,
,半径为1,
过点M作直线![]() 垂线,垂足为D,交⊙D于C点,如图:
垂线,垂足为D,交⊙D于C点,如图:
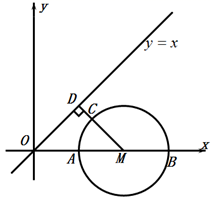
此时![]() 取得最小值,
取得最小值,
∵直线的解析式为:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 最小值为
最小值为![]() ,
,
故答案为:![]() .
.
【点睛】
本题考查了点的轨迹,圆周角定理,圆心到直线的距离,正确理解点到直线的距离垂线段最短是正确解答本题的关键.
圆的半径为5cm,如果圆心到直线的距离为3cm,那么直线与圆有公共点的个数是_____.
2
【解析】
根据直线与圆的位置关系定理:相切时,r=d;相交时r>d;相离时,r<d;进行判断即可.
【详解】
解:∵圆的半径为5cm,圆心到一条直线的距离是3cm,
3<5,
即半径大于圆心到直线的距离,
∴直线与圆的位置关系是相交,
即直线与圆有2个交点.
故答案为2.
【点睛】
本题主要考查对直线与圆的位置关系的理解和掌握,能熟练地根据定理进行说理是解此题的关键.
已知Rt△ABC中,![]() ,
,![]() ,
,![]() ,如果以点
,如果以点![]() 为圆心的圆与斜边
为圆心的圆与斜边![]() 有唯一的公共点,那么
有唯一的公共点,那么![]() 的半径
的半径![]() 的取值范围为____.
的取值范围为____.
![]() 或
或![]()
【分析】
因为要使圆与斜边只有一个公共点,所以该圆和斜边相切或和斜边相交,但只有一个交点在斜边上.若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
【详解】
根据勾股定理求得BC=![]() =6,
=6,
当圆和斜边相切时,则半径即是斜边上的高,等于![]() ;
;
当圆和斜边相交,且只有一个交点在斜边上时,可以让圆的半径大于短直角边而小于长直角边,则6<r≤8,
故半径r的取值范围是r=4.8或6<r≤8,
故答案为r=4.8或6<r≤8.
【点睛】
此题考查了直线与圆的位置关系,此题注意考虑两种情况,只需保证圆和斜边只有一个公共点即可.
本卷还有95题,登录并加入会员即可免费使用哦~

该作品由: 用户徐开鹏分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。