初中数学2021年初专题周练——特殊的平行四边形训练题（一）【含详解】
初中
整体难度：偏难
2021-01-21
题号
一
二
三
四
五
评分
一、选择题 (共41题)
添加该题型下试题
1.
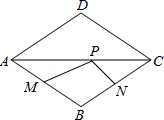
如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边上的中点，则MP+PN的最小值是（ ）
A．
B．1 C．
D．2
难度：
知识点：特殊的平行四边形
使用次数：284
【答案】
B
【分析】
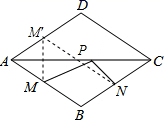
先作点M关于AC的对称点M′，连接M′N交AC于P，此时MP+NP有最小值．然后证明四边形ABNM′为平行四边形，即可求出MP+NP=M′N=AB=1．
【详解】
解：如图
，
作点M关于AC的对称点M′，连接M′N交AC于P，此时MP+NP有最小值，最小值为M′N的长．
∵菱形ABCD关于AC对称，M是AB边上的中点，
∴M′是AD的中点，
又∵N是BC边上的中点，
∴AM′∥BN，AM′=BN，
∴四边形ABNM′是平行四边形，
∴M′N=AB=1，
∴MP+NP=M′N=1，即MP+NP的最小值为1，
故选B．
2.
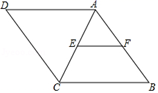
如图，在菱形ABCD中，E是AC的中点，EF∥CB，交AB于点F，如果EF=3，那么菱形ABCD的周长为（ ）
A．24 B．18 C．12 D．9
难度：
知识点：平行四边形
使用次数：210
【答案】
A
【解析】易得BC长为EF长的2倍，那么菱形ABCD的周长=4BC问题得解．
【详解】∵E是AC中点，
∵EF∥BC，交AB于点F，
∴EF是△ABC的中位线，
∴BC=2EF=2×3=6，
∴菱形ABCD的周长是4×6=24，
故选A．
【点睛】本题考查了三角形中位线的性质及菱形的周长公式，熟练掌握相关知识是解题的关键.
3.
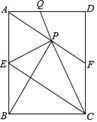
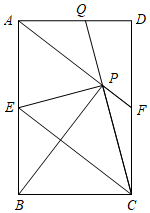
如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP并延长AP交CD于F点，连结CP并延长CP交AD于Q点．给出以下结论：
①四边形AECF为平行四边形；
②∠PBA=∠APQ；
③△FPC为等腰三角形；
④△APB≌△EPC；
其中正确结论的个数为（ ）
A．1 B．2 C．3 D．4
难度：
知识点：平行四边形
使用次数：241
【答案】
B
【解析】
分析：①根据三角形内角和为180°易证∠PAB+∠PBA=90°，易证四边形AECF是平行四边形，即可解题；
②根据平角定义得：∠APQ+∠BPC=90°，由正方形可知每个内角都是直角，再由同角的余角相等，即可解题；
③根据平行线和翻折的性质得：∠FPC=∠PCE=∠BCE，∠FPC≠∠FCP，且∠PFC是钝角，△FPC不一定为等腰三角形；
④当BP=AD或△BPC是等边三角形时，△APB≌△FDA，即可解题．
详解：①如图，EC，BP交于点G；
∵点P是点B关于直线EC的对称点，
∴EC垂直平分BP，
∴EP=EB，
∴∠EBP=∠EPB，
∵点E为AB中点，
∴AE=EB，
∴AE=EP，
∴∠PAB=∠PBA，
∵∠PAB+∠PBA+∠APB=180°，即∠PAB+∠PBA+∠APE+∠BPE=2（∠PAB+∠PBA）=180°，
∴∠PAB+∠PBA=90°，
∴AP⊥BP，
∴AF∥EC；
∵AE∥CF，
∴四边形AECF是平行四边形，
故①正确；
②∵∠APB=90°，
∴∠APQ+∠BPC=90°，
由折叠得：BC=PC，
∴∠BPC=∠PBC，
∵四边形ABCD是正方形，
∴∠ABC=∠ABP+∠PBC=90°，
∴∠ABP=∠APQ，
故②正确；
③∵AF∥EC，
∴∠FPC=∠PCE=∠BCE，
∵∠PFC是钝角，
当△BPC是等边三角形，即∠BCE=30°时，才有∠FPC=∠FCP，
如右图，△PCF不一定是等腰三角形，
故③不正确；
④∵AF=EC，AD=BC=PC，∠ADF=∠EPC=90°，
∴Rt△EPC≌△FDA（HL），
∵∠ADF=∠APB=90°，∠FAD=∠ABP，
当BP=AD或△BPC是等边三角形时，△APB≌△FDA，
∴△APB≌△EPC，
故④不正确；
其中正确结论有①②，2个，
故选B．
点睛：本题考查了全等三角形的判定和性质，等腰三角形的性质和判定，矩形的性质，翻折变换，平行四边形的判定，熟练掌握全等三角形的判定与性质是解本题的关键．
4.
下列命题中，真命题是（ ）
A．对角线相等的四边形是矩形
B．对角线互相垂直的四边形是菱形
C．对角线互相平分的四边形是平行四边形
D．对角线互相垂直平分的四边形是正方形
难度：
知识点：平行四边形
使用次数：119
【答案】
C
【解析】
试题分析：A、两条对角线相等且相互平分的四边形为矩形；故本选项错误；
B、对角线互相垂直的平行四边形是菱形；故本选项错误；
C、对角线互相平分的四边形是平行四边形；故本选项正确；
D、对角线互相垂直平分且相等的四边形是正方形；故本选项错误．
故选C．
5.
如图，在正方形ABCD中，AB=9，点E在CD边上，且DE=2CE，点P是对角线AC上的一个动点，则PE+PD的最小值是（ ）
A．
B．
C．9 D．
难度：
知识点：特殊的平行四边形
使用次数：220
【答案】
A
【解析】
解：如图，连接BE，设BE与AC交于点P′，∵四边形ABCD是正方形，∴点B与D关于AC对称，∴P′D=P′B，∴P′D+P′E=P′B+P′E=BE最小．即P在AC与BE的交点上时，PD+PE最小，为BE的长度．∵直角△CBE中，∠BCE=90°，BC=9，CE=
CD=3，∴BE=
=
．故选A．
点睛：此题考查了轴对称﹣﹣最短路线问题，正方形的性质，要灵活运用对称性解决此类问题．找出P点位置是解题的关键．
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
偏难
难度统计
难度系数
数量
占比
中等
57
56.99%
偏难
33
33.0%
容易
7
7.00%
基础
1
1.0%
很难
2
2.0%
题型统计
大题类型
数量
占比
选择题
41
41.0%
解答题
44
44.0%
填空题
15
15.0%
知识点统计
知识点
数量
占比
特殊的平行四边形
63
63.0%
平行四边形
15
15.0%
图形的旋转
2
2.0%
相似三角形
4
4.0%
直射、射线、线段
1
1.0%
三角形全等的判定
6
6.0%
实际问题与二次函数
1
1.0%
等腰三角形
2
2.0%
全等三角形
2
2.0%
课题学习 最短路径问题
1
1.0%
一次函数
1
1.0%
与三角形有关的线段
1
1.0%
平面直角坐标系
1
1.0%
版权提示
该作品由: 用户喻鹤芸分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。