初中数学2021年初周练知识点——分式的运算训练题（一）【含详解】
初中
整体难度：中等
2021-01-11
题号
一
二
三
四
五
评分
一、选择题 (共32题)
添加该题型下试题
1.
老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：
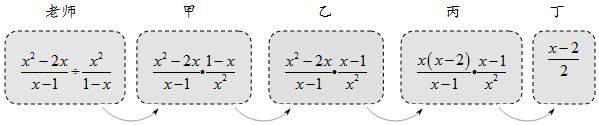
接力中，自己负责的一步出现错误的是（ ）
A．只有乙 B．甲和丁 C．乙和丙 D．乙和丁
难度：
知识点：分式的运算
使用次数：165
【答案】
D
【解析】
根据分式的乘除运算步骤和运算法则逐一计算即可判断．
【详解】∵
=
=
=
=
=
，
∴出现错误是在乙和丁，
故选D．
【点睛】本题考查了分式的乘除法，熟练掌握分式乘除法的运算法则是解题的关键.
2.
如果
，那么代数式
的值为
A．
B．
C．
D．
难度：
知识点：分式的运算
使用次数：177
【答案】
A
【解析】
分析：根据分式混合运算的法则进行化简，再把
整体代入即可.
详解：原式
，
∵，
∴原式
．
故选A.
点睛：考查分式的化简求值，熟练掌握分式混合运算的法则是解题的关键.
3.
对于任意的x值都有
，则M，N值为（ ）
A．M＝1，N＝3 B．M＝﹣1，N＝3 C．M＝2，N＝4 D．M＝1，N＝4
难度：
知识点：分式的运算
使用次数：125
【答案】
B
【分析】
先计算
=
,根据已知可得关于M、N的二元一次方程组
，解之可得．
【详解】
解：
=
=
∴
=
∴，
解得：
，
故选B．
【点睛】
本题主要考查分式的加减法，解题的关键是熟练掌握分式的加减法则，并根据已知等式得出关于M、N的方程组．
4.
计算
的结果为
A．
B．
C．
D．
难度：
知识点：分式的运算
使用次数：141
【答案】
A
【解析】
先计算（-a）2，然后再进行约分即可得.
【详解】
=
=b，
故选A.
【点睛】本题考查了分式的乘法，熟练掌握分式乘法的运算法则是解题的关键.
5.
已知
，则
的值是
A．
B．－ C．2 D．－2
难度：
知识点：分式的运算
使用次数：176
【答案】
D
【解析】
分析：观察已知和所求的关系，容易发现把已知通分后，再求倒数即可．
解答：解：∵
，
∴
-
=
，
∴
=，
∴
=-2．
故选D．
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
中等
难度统计
难度系数
数量
占比
中等
56
56.00%
容易
17
17.0%
偏难
23
23.0%
基础
4
4.0%
题型统计
大题类型
数量
占比
选择题
32
32.0%
解答题
52
52.0%
填空题
16
16.0%
知识点统计
知识点
数量
占比
分式的运算
87
87.0%
有理数的乘除法
2
2.0%
整式的加减
2
2.0%
（补充）整式的除法
3
3.0%
整式
2
2.0%
实数
1
1.0%
整式的乘法
1
1.0%
有理数
1
1.0%
分式
1
1.0%
版权提示
该作品由: 用户上官雪君分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。