实数![]() 的平方根是( )
的平方根是( )
A.±3 B.![]() C.﹣3 D.3
C.﹣3 D.3
B
【分析】
直接利用平方根的定义计算即可得到答案.
【详解】
解:∵![]() ,
,
![]() 的平方是3,
的平方是3,
∴![]() 的平方根是
的平方根是![]() .
.
故选:B.
【点睛】
此题主要考查了平方根的定义:如果一个数的平方等于a,这个数就叫做a的平方根,也叫做a的二次方根.注意:一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.
实数a、b在数轴上的位置如图,则![]() 等于
等于![]()
![]()
![]()
A.2a B.2b C.![]() D.
D.![]()
A
【详解】
根据实数a、b在数轴上的位置得知:
a<0,b>0,a+b>0, a﹣b<0
∴|a+b|=a+b,|a﹣b|=b﹣a,
∴|a+b|-|a﹣b|=a+b-b+a=2a,
故选A.
在-![]() ,0,-|-5|,-0.6,2,
,0,-|-5|,-0.6,2,![]() ,-10中负数的个数有( )
,-10中负数的个数有( )
A.3 B.4 C.5 D.6
B
【分析】
先化简,再根据负数的定义判断即可.
【详解】
-![]() -|-5|=-5是负数,-0.6是负数,-10是负数,故负数为4个.
-|-5|=-5是负数,-0.6是负数,-10是负数,故负数为4个.
【点睛】
本题考查负数的判断,解题的关键是清楚负数的定义.
在同一平面直角坐标系中,函数y=ax+b与y=ax2﹣bx的图象可能是( )
A. B.
B.
C.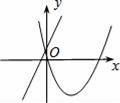 D.
D.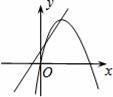
C
【解析】
试题分析:选项A:一次函数图像经过一、二、三象限,因此a>0,b>0,对于二次函数y=ax2﹣bx图像应该开口向上,对称轴在y轴右侧,不合题意,此选项错误;选项B:一次函数图像经过一、二、四象限,因此a<0,b>0,对于二次函数y=ax2﹣bx图像应该开口向下,对称轴在y轴左侧,不合题意,此选项错误;
选项C:一次函数图像经过一、二、三象限,因此a>0,b>0,对于二次函数y=ax2﹣bx图像应该开口向上,对称轴在y轴右侧,符合题意,此选项正确;选项D:一次函数图像经过一、二、三象限,因此a>0,b>0,对于二次函数y=ax2﹣bx图像应该开口向上,对称轴在y轴右侧,不合题意,此选项错误.故选C.
考点:1一次函数图像;2二次函数图像.
已知平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )
A.﹣3 B.﹣5 C.1或﹣3 D.1或﹣5
A
【解析】
分析:根据点A(a+2,4)和B(3,2a+2)到x轴的距离相等,得到4=|2a+2|,即可解答.
详解:∵点A(a+2,4)和B(3,2a+2)到x轴的距离相等,
∴4=|2a+2|,a+2≠3,
解得:a=−3,
故选A.
点睛:考查点的坐标的相关知识;用到的知识点为:到x轴和y轴的距离相等的点的横纵坐标相等或互为相反数.
本卷还有17题,登录并加入会员即可免费使用哦~

该作品由: 用户邓婕分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。