计算![]() 的结果等于( )
的结果等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
A
【分析】
有理数的乘法计算,根据两个有理数相乘的乘法法则进行计算求解即可.
【详解】
解:![]()
故选:A.
【点睛】
本题考查有理数的乘法,掌握两个有理数相乘的计算法则是本题的解题关键.
sin60°=( )
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
D
【解析】
根据特殊三角函数值即可得sin60°=![]() ,故选D.
,故选D.
下列图案中,是中心对称图形但不是轴对称图形的是 ( )
A. B.
B. C.
C. D.
D.
C
【解析】
根据中心对称图形以及轴对称图形的概念逐一进行分析即可得.
【详解】
A、不是中心对称图形,是轴对称图形,故不符合题意;
B、是轴对称图形,也是中心对称图形,故不符合题意;
C、是中心对称图形,不是轴对称图形,故符合题意;
D、不是中心对称图形,也不是轴对称图形,故不符合题意,
故选C.
【点睛】
本题主要考查轴对称图形和中心对称图形,在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形;在平面内,如果把一个图形绕某个点旋转180°后,能与原图形重合,那么就说这个图形是中心对称图形.
北京大兴国际机场主航站楼和配套服务楼、停车楼总建筑规模约![]() .
.![]() 用科学记数法表示应为( )
用科学记数法表示应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
C
【分析】
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【详解】
解:![]() =
=![]()
故选:C.
【点睛】
此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
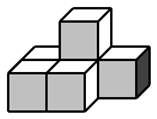
如图是一个由![]() 个相同的正方体组成的立体图形,它的主视图是( )
个相同的正方体组成的立体图形,它的主视图是( )
A.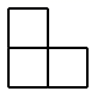 B.
B.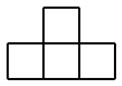
C. D.
D.
B
【分析】
找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
【详解】
解:从正面看易得第一层有3个正方形,第二层有1个正方形并位于中间位置.
故选:B.
【点睛】
本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
本卷还有45题,登录并加入会员即可免费使用哦~

该作品由: 用户yet分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。