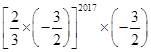初中数学2020年年末周练知识点——有理数的乘方训练题（一）【含详解】
初中
整体难度：偏难
2021-01-05
题号
一
二
三
四
五
评分
一、选择题 (共49题)
添加该题型下试题
C
D
2.
下列各组数中，互为相反数的是( )
A．-（-1）与1 B．（－1）2与1 C．
与1 D．－12与1
难度：
知识点：有理数
使用次数：149
【答案】
D
【解析】
试题分析:选项A，-（-1）与1不是相反数，选项A错误；选项B，（－1）2与1不是互为相反数，选项B错误；选项C，｜-1｜与1不是相反数，选项C错误；选项D，－12与1是相反数，选项正确．故答案选D．
考点：相反数．
3.
下列说法：①
一定是负数；②
一定是正数；③倒数等于它本身的数是
；④绝对值等于它本身的数是l；⑤平方等于它本身的数是1．其中正确的个数是（ ）
A．1个 B．2个 C．3个 D．4个
难度：
知识点：正数和负数
使用次数：189
【答案】
A
【分析】
根据正数与负数的意义对①进行判断即可；根据绝对值的性质对②与④进行判断即可；根据倒数的意义对③进行判断即可；根据平方的意义对⑤进行判断即可.
【详解】
①
不一定是负数，故该说法错误；
②
一定是非负数，故该说法错误；
③倒数等于它本身的数是
，故该说法正确；
④绝对值等于它本身的数是非负数，故该说法错误；
⑤平方等于它本身的数是0或1，故该说法错误．
综上所述，共1个正确，
故选：A.
【点睛】
本题主要考查了有理数的性质，熟练掌握相关概念是解题关键.
4.
（-2）2004+3×（-2）2003的值为 （ ）
A．-22003 B．22003 C．-22004 D．22004
难度：
知识点：有理数的乘方
使用次数：148
【答案】
A
【解析】
（-2）2004可以表示为（-2）（-2）2003，可以提取（-2）2003，即可求解．
解：原式=（-2）（-2）2003+3×（-2）2003，
=（-2）2003（-2+3），
=（-2）2003，
=-22003．
故选A．
点评：本题主要考查了有理数的乘方的性质，（-a）2n=a2n，（-a）2n+1=-a2n+1，正确提取是解决本题的关键．
B
C
D
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
偏难
难度统计
难度系数
数量
占比
中等
43
43.0%
容易
13
13.0%
偏难
33
33.0%
基础
10
10.0%
很难
1
1.0%
题型统计
大题类型
数量
占比
选择题
49
49.0%
填空题
28
28.00%
解答题
23
23.0%
知识点统计
知识点
数量
占比
有理数的乘方
66
66.0%
有理数
28
28.00%
正数和负数
2
2.0%
有理数的加减法
2
2.0%
有理数的乘除法
2
2.0%
版权提示
该作品由: 用户小小分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。