如图,正方形ABCD内接于⊙O,AB=2![]() ,则
,则![]() 的长是( )
的长是( )

A.π B.![]() π C.2π D.
π C.2π D.![]() π
π
A
【解析】连接OA、OB,求出∠AOB=90°,根据勾股定理求出AO,根据弧长公式求出即可.
【详解】连接OA、OB,
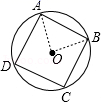
∵正方形ABCD内接于⊙O,
∴AB=BC=DC=AD,
∴![]() ,
,
∴∠AOB=![]() ×360°=90°,
×360°=90°,
在Rt△AOB中,由勾股定理得:2AO2=(2![]() )2,
)2,
解得:AO=2,
∴![]() 的长为
的长为![]() =π,
=π,
故选A.
【点睛】本题考查了弧长公式和正方形的性质,求出∠AOB的度数和OA的长是解此题的关键.
如图,正六边形ABCDEF内接于⊙O,连接BD.则∠CBD的度数是( )
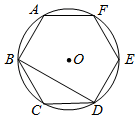
A.30° B.45° C.60° D.90°
A
【分析】
根据正六边形的内角和求得∠BCD,然后根据等腰三角形的性质即可得到结论.
【详解】
∵在正六边形ABCDEF中,∠BCD=![]() =120°,BC=CD,
=120°,BC=CD,
∴∠CBD=![]() (180°﹣120°)=30°,
(180°﹣120°)=30°,
故选A.
【点睛】
本题考查的是正多边形和圆、等腰三角形的性质,三角形的内角和,熟记多边形的内角和是解题的关键.
如图,已知正五边形![]() 内接于
内接于![]() ,连结
,连结![]() ,则
,则![]() 的度数是( )
的度数是( )
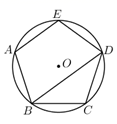
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
C
【分析】
根据多边形内角和定理、正五边形的性质求出∠ABC、CD=CB,根据等腰三角形的性质求出∠CBD,计算即可.
【详解】
∵五边形![]() 为正五边形
为正五边形
∴![]()
∵![]()
∴![]()
∴![]()
故选C.
【点睛】
本题考查的是正多边形和圆、多边形的内角和定理,掌握正多边形和圆的关系、多边形内角和等于(n-2)×180°是解题的关键.
下列图形为正多边形的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.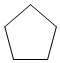
D
【解析】
根据正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形可得答案.
【详解】
根据正多边形的定义,得到D中图形是正五边形.
故选D.
【点睛】
本题考查了正多边形,关键是掌握正多边形的定义.
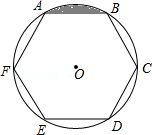
如图,ABCDEF为⊙O的内接正六边形,AB=a,则图中阴影部分的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
B
【解析】利用圆的面积公式和三角形的面积公式求得圆的面积和正六边形的面积,阴影面积=![]() (圆的面积﹣正六边形的面积),即可得出结果.
(圆的面积﹣正六边形的面积),即可得出结果.
【详解】∵正六边形的边长为a,
∴⊙O的半径为a,
∴⊙O的面积为π×a2=πa2,
∵空白正六边形为六个边长为a的正三角形,
∴每个三角形面积为![]() ×a×a×sin60°=
×a×a×sin60°=![]() a2,
a2,
∴正六边形面积为6×![]() a2=
a2=![]() a2,
a2,
∴阴影面积为(πa2﹣![]() a2)×
a2)×![]() =(
=(![]() ﹣
﹣![]() )a2,
)a2,
故选B.
【点睛】本题主要考查了正多边形和圆的面积公式,注意到阴影面积=![]() (圆的面积﹣正六边形的面积)是解答此题的关键.
(圆的面积﹣正六边形的面积)是解答此题的关键.
本卷还有95题,登录并加入会员即可免费使用哦~

该作品由: 用户小小分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。