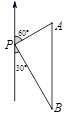
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B与灯塔P之间的距离为( )
A.60海里 B.45海里 C.20![]() 海里 D.30
海里 D.30![]() 海里
海里
D
【分析】
根据题意得出:∠B=30°,AP=30海里,∠APB=90°,再利用勾股定理得出BP的长,求出答案.
【详解】
解:由题意可得:∠B=30°,AP=30海里,∠APB=90°,
故AB=2AP=60(海里),
则此时轮船所在位置B处与灯塔P之间的距离为:BP=![]() (海里)
(海里)
故选:D.
【点睛】
此题主要考查了勾股定理的应用以及方向角,正确应用勾股定理是解题关键.
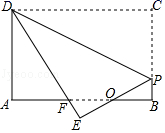
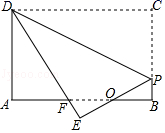
如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
C
【解析】
根据折叠的性质可得出DC=DE、CP=EP,由∠EOF=∠BOP、∠B=∠E、OP=OF可得出△OEF≌△OBP(AAS),根据全等三角形的性质可得出OE=OB、EF=BP,设EF=x,则BP=x、DF=4﹣x、BF=PC=3﹣x,进而可得出AF=1+x,在Rt△DAF中,利用勾股定理可求出x的值,再利用余弦的定义即可求出cos∠ADF的值.
【详解】
根据折叠,可知:△DCP≌△DEP,
∴DC=DE=4,CP=EP.
在△OEF和△OBP中,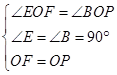 ,
,
∴△OEF≌△OBP(AAS),
∴OE=OB,EF=BP.
设EF=x,则BP=x,DF=DE﹣EF=4﹣x,
又∵BF=OB+OF=OE+OP=PE=PC,PC=BC﹣BP=3﹣x,
∴AF=AB﹣BF=1+x.
在Rt△DAF中,AF2+AD2=DF2,即(1+x)2+32=(4﹣x)2,
解得:x=![]() ,
,
∴DF=4﹣x=![]() ,
,
∴cos∠ADF=![]() ,
,
故选C.
【点睛】
本题考查了全等三角形的判定与性质、勾股定理以及解直角三角形,利用勾股定理结合AF=1+x,求出AF的长度是解题的关键.
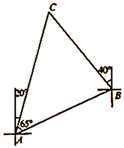
如图,一艘船由![]() 港沿北偏东65°方向航行
港沿北偏东65°方向航行![]() 至
至![]() 港,然后再沿北偏西40°方向航行至
港,然后再沿北偏西40°方向航行至![]() 港,
港,![]() 港在
港在![]() 港北偏东20°方向,则
港北偏东20°方向,则![]() ,
,![]() 两港之间的距离为( )
两港之间的距离为( )![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
B
【分析】
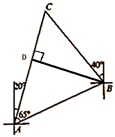
根据题意作BD垂直于AC于点D,根据计算可得![]() ,
,![]() ;根据直角三角形的性质求解即可.
;根据直角三角形的性质求解即可.
【详解】
解:根据题意作BD垂直于AC于点D.可得AB=![]() ,
,![]()
![]()
所以可得![]()
![]()
![]()
因此可得![]()
故选B.
【点睛】
本题主要考查解直角三角形的应用,根据特殊角的三角函数值计算即可.
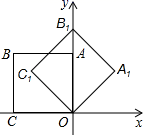
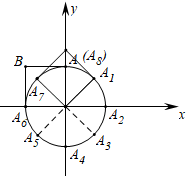
如图,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转![]() 后得到正方形
后得到正方形![]() ,依此方式,绕点O连续旋转2019次得到正方形
,依此方式,绕点O连续旋转2019次得到正方形![]() ,那么点
,那么点![]() 的坐标是( )
的坐标是( )
A.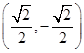 B.
B.![]() C.
C.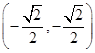 D.
D.![]()
A
【分析】
根据旋转的性质分别求出点A1、A2、A3、…的坐标,继而发现8次为一个循环,用2019除以8,看余数即可求得答案.
【详解】
![]() 四边形OABC是正方形,且
四边形OABC是正方形,且![]() ,
,
![]() ,
,
![]() 将正方形OABC绕点O逆时针旋转
将正方形OABC绕点O逆时针旋转![]() 后得到正方形
后得到正方形![]() ,
,
∴点A1的横坐标为1![]() ,点A1的纵坐标为1
,点A1的纵坐标为1![]() ,
,
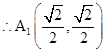 ,
,
继续旋转则![]() ,
,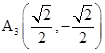 ,A4(0,-1),A5
,A4(0,-1),A5 ,A6(-1,0),A7
,A6(-1,0),A7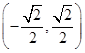 ,A8(0,1),A9
,A8(0,1),A9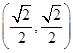 ,……,
,……,
发现是8次一循环,所以![]() …余3,
…余3,
![]() 点
点![]() 的坐标为
的坐标为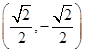 ,
,
故选A.
【点睛】
本题考查了旋转的性质,规律题——点的坐标的变化规律,通过分析正确得出坐标的变化规律是解题的关键.
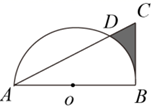
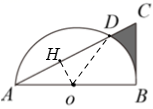
如图,在Rt△ABC中,∠ABC=90°,AB=![]() ,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
A
【解析】
连接OD,过点O作OH⊥AC,垂足为 H,则有AD=2AH,∠AHO=90°,在Rt△ABC中,利用∠A的正切值求出∠A=30°,继而可求得OH、AH长,根据圆周角定理可求得∠BOC =60°,然后根据S阴影=S△ABC-S△AOD-S扇形BOD进行计算即可.
【详解】
连接OD,过点O作OH⊥AC,垂足为 H,
则有AD=2AH,∠AHO=90°,
在Rt△ABC中,∠ABC=90°,AB=![]() ,BC=2,tan∠A=
,BC=2,tan∠A=![]() ,
,
∴∠A=30°,
∴OH=![]() OA=
OA=![]() ,AH=AO•cos∠A=
,AH=AO•cos∠A=![]() ,∠BOC=2∠A=60°,
,∠BOC=2∠A=60°,
∴AD=2AH=![]() ,
,
∴S阴影=S△ABC-S△AOD-S扇形BOD=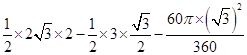 =
=![]() ,
,
故选A.
【点睛】
本题考查了垂径定理,圆周角定理,扇形面积,解直角三角形等知识,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.
本卷还有95题,登录并加入会员即可免费使用哦~

该作品由: 用户左济荣分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。