2019重庆人教版初中数学中考模拟137898
初中
整体难度：中等
2020-11-30
题号
一
二
三
四
五
评分
一、选择题 (共12题)
添加该题型下试题
1.
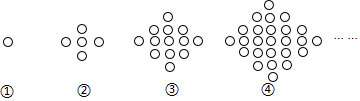
观察下列图形，①中有1个圆，②中有5个圆，③中有13个圆……，若依此规律，则第⑥个图形中圆的个数为（ ）
A．25 B．61 C．41 D．65
难度：
知识点：整式
使用次数：107
【答案】
B
【解析】
仔细观察图形，找到图形的变化规律，利用规律解得即可．
【详解】
第一个图形有1个圆，
第二个图形有1+3+1＝5个圆，
第三个图形有1+3+5+3+1＝13个圆，
第四个图形有1+3+5+7+5+3+1＝25个圆，
…
第六个图形有1+3+5+7+9+11+9+7+5+3+1＝61个圆，
故选：B．
【点睛】
此题考查图形的变化规律，找出图形之间的运算规律，利用规律解决问题．
2.
已知抛物线y＝﹣x2+（k﹣1）x+3，当x＞2时，y随x的增大而减小，并且关于x的分式方程
的解为正数．则符合条件的所有正整数k的和为（ ）
A．8 B．10 C．13 D．15
难度：
知识点：分式方程
使用次数：123
【答案】
C
【解析】
根据抛物线图象先求出k的取值范围，再解分式方程，根据分式方程的解确定k的值，继而求出答案．
【详解】
解：∵
∴抛物线对称轴为
，抛物线开口向下，
∵当
时y随着x的增大而减小，
∴
，
解得：
，
解关于x的分式方程
可得：
，且
，则
，
∵分式方程的解是正数，
∴符合条件的正整数k为：
∴符合条件的整数k的和为：
．
故选：C．
【点睛】
本题考查的知识点是二次函数图象及其性质以及解分式方程，解此题的关键是掌握二次函数图象的性质．
3.
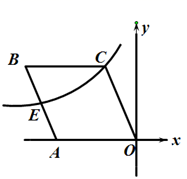
如图，在平面直角坐标系中，菱形
的一边
在
轴上，
，反比例函数
过菱形的顶点
和
边上的中点
，则
的值为（ ）
A．-4 B．
C．-5 D．
难度：
知识点：反比例函数单元测试
使用次数：123
【答案】
B
【解析】
作
，
，可将点C的坐标设出来，然后根据点C的坐标表示出点E的坐标，因为点E也在反比例函数图像上，代入即可求出C的坐标，然后在
中利用勾股定理即可求出k的值.
【详解】
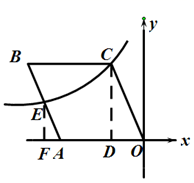
如图，作，，
，
设点横坐标为
，即
，
∵四边形
为菱形，边长为3，E为AB中点
∴点坐标为
；
代入
得：
，
∴
，
在
中，
，
，
解得：
，
又∵
，
∴
.
故选B
【点睛】
本题主要考查了待定系数法求反比例函数的解析式及相似三角形的判定及性质，能够根据点C的坐标写出点E的坐标是解题的关键.
4.
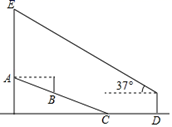
春天是放风筝的好时节，小明为了让风筝顺利起飞，特地将风筝放在坡度为1：2.4的山坡上，并站在视线刚好与风筝起飞点A齐平的B处，起风后小明开始往下跑26米至坡底C处，并继续沿平地向前跑16米到达D处后站在原地开始调整，小明将手中的线轴刚好举到与视线齐平处测得风筝的仰角是37°，此时风筝恰好升高到起飞时的正上方E处．已知小明视线距地面高度为1.5米，图中风筝E、A、B、C、D五点在同一平面，则风筝上升的垂直距离AE约为（ ）米．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
A．34.2 B．32.7 C．31.2 D．22.7
难度：
知识点：解直角三角形与其应用
使用次数：150
【答案】
D
【解析】
根据AN∥SC，则
，求出：AN＝3.6＝RS，AR＝NS＝BS＋NB，则AM＝10，RD＝RS＋SC＋CD＝3.6＋24＋16＝43.6＝MG，EM＝MGtan37°＝32.7，最后根据AE＝EM−AM，即可求解．
【详解】
解：设小明在B处视线的点为N，延长NB交CD于点S，过点G作GM平行于地面交AE于点M，
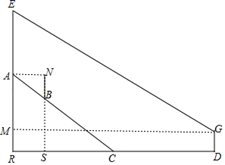
坡度为1：2.4，BC＝26，则BC＝10，SC＝24，BS＝10，
∵AN∥SC，∴，
即：
，解得：AN＝3.6＝RS，
AR＝NS＝BS+NB＝10+1.5＝11.5，则AM＝10，
RD＝RS+SC+CD＝3.6+24+16＝43.6＝MG，
EM＝MGtan37°＝32.7，
AE＝EM﹣AM＝32.7﹣10＝22.7，
故选：D．
【点睛】
本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．
5.
如图，直线l与⊙O相切于点A，直径BC的延长线与切线l交于点D，连接AB．且∠BDA＝3∠DBA，则∠DBA的度数为（ ）
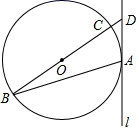
A．15° B．20° C．18° D．22°
难度：
知识点：点和圆、直线和圆的位置关系
使用次数：179
【答案】
C
【解析】
连接OA，根据等腰三角形的性质得到∠OBA=∠OAB，由三角形的外角性质得到∠DOA=2∠OBA，设∠DBA=α，根据三角形的内角和即可得出结果．
【详解】
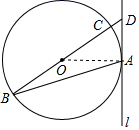
解：如图所示，连接OA．
∵OB＝OA，
∴∠OBA＝∠OAB，
∴∠DOA＝2∠OBA，
∵∠BDA＝3∠DBA，
∴设∠DBA＝α，
∴∠DOA＝2α，∠ADB＝3α，
∵AD是⊙的切线，
∴∠OAD＝90°．
∴2α+3α＝90°，
∴α＝18°．
∴∠DBA＝18°，
故选：C．
【点睛】
本题主要考查的是切线的性质、等腰三角形的性质以及三角形的外角性质等知识点，掌握以上知识点是解题的关键．
本卷还有21题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
26
总体难度：
中等
难度统计
难度系数
数量
占比
容易
7
26.92%
很难
1
3.84%
中等
13
50.0%
偏难
2
7.69%
基础
3
11.53%
题型统计
大题类型
数量
占比
选择题
12
46.15%
解答题
8
30.76%
填空题
6
23.07%
知识点统计
知识点
数量
占比
整式
1
3.84%
二次函数单元测试
1
3.84%
分式的运算
1
3.84%
特殊的平行四边形
2
7.69%
等腰三角形
1
3.84%
（补充）整式的除法
1
3.84%
三元一次方程组的解法
1
3.84%
弧长和扇形面积
1
3.84%
数据的波动程度
1
3.84%
锐角三角函数
1
3.84%
分式方程
1
3.84%
反比例函数单元测试
1
3.84%
解直角三角形与其应用
1
3.84%
点和圆、直线和圆的位置关系
1
3.84%
实数单元测试
1
3.84%
二次根式的乘除
1
3.84%
图形的相似
1
3.84%
立方根
1
3.84%
几何图形
1
3.84%
二次函数与一元二次方程
1
3.84%
函数
2
7.69%
直方图
1
3.84%
实际问题与一元二次方程
1
3.84%
轴对称
1
3.84%
版权提示
该作品由: 用户霖分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。