2020重庆人教版初中数学中考模拟120718
初中
整体难度：中等
2020-11-16
题号
一
二
三
四
五
评分
一、选择题 (共12题)
添加该题型下试题
1.
由落户重庆两江新区数字经济产业园的跨境电商服务平台签订的对日本的订单中，首批1200000只“重庆造”一次性防护口罩于5月15日运抵日本，数据1200000用科学记数法表示为（ ）．
A．1.2×105 B．1.2×106 C．0.12×107 D．12×105
难度：
知识点：有理数的乘除法
使用次数：167
【答案】
B
【解析】
科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数；确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【详解】
将1200000用科学记数法表示为1.2×106
故选：B．
【点睛】
本题考察了科学记数法的知识；求解的关键是准确掌握科学记数法的性质．
2.
正方形的面积是4，则它的对角线长是（ ）
A．2 B．
C．
D．4
难度：
知识点：勾股定理
使用次数：142
【答案】
C
【解析】
设正方形的对角线为x，然后根据勾股定理列式计算即可得解．
【详解】
解：设正方形的对角线为x，
∵正方形的面积是4，
∴边长的平方为4，
∴由勾股定理得，x＝
＝2．
故选：C．
【点睛】
本题主要考查勾股定理，熟练掌握勾股定理是解题的关键．
3.
实数a，b，c在数轴上的对应点的位置如图所示，则正确的结论是（ ）
A．|a|＜4 B．abc＜0 C．b﹣c＞0 D．a+c＞0
难度：
知识点：有理数
使用次数：104
【答案】
A
【解析】
由图可知，a、b、c绝对值之间的大小关系，从而判断四个选项的对错．
【详解】
观察数轴可知：a＜b＜0＜c，且|b|＜|c|＜|a|；
所以abc＜0，b﹣c＞0，a+c＞0是错误的；|a|＜4是正确的；
故选：A．
【点睛】
主要考查数轴、绝对值以及实数及其运算，观察数轴是解题的关键．
4.
若
＝
（a≠0，b≠0），则
＝（ ）
A．
B．
C．
D．
难度：
知识点：图形的相似
使用次数：137
【答案】
D
【解析】
直接把已知代入进而化简得出答案．
【详解】
解：∵＝（a≠0，b≠0），
∴4a＝3b，
故a＝
b，
则＝ 
＝．
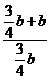故选：D．
【点睛】
本题考查了比例的性质，正确得出a、b的关系是解题的关键．
5.
如图，Rt△ABC中，∠C＝90°，∠B＝30°，分别以点A和点B为圆心，大于
的长为半径作弧，两弧相交于M、N两点，作直线MN，交BC于点D，连接AD，则∠CAD的度数是( )
A．20° B．30° C．45° D．60°
难度：
知识点：课题学习 最短路径问题
使用次数：149
【答案】
B
【解析】
根据内角和定理求得∠BAC=60°，由中垂线性质知DA=DB，即∠DAB=∠B=30°，从而得出答案．
【详解】
在△ABC中，∵∠B=30°，∠C=90°，
∴∠BAC=180°-∠B-∠C=60°，
由作图可知MN为AB的中垂线，
∴DA=DB，
∴∠DAB=∠B=30°，
∴∠CAD=∠BAC-∠DAB=30°，
故选B．
【点睛】
本题主要考查作图-基本作图，熟练掌握中垂线的作图和性质是解题的关键．
本卷还有21题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
26
总体难度：
中等
难度统计
难度系数
数量
占比
基础
3
11.53%
容易
8
30.76%
中等
11
42.30%
偏难
2
7.69%
很难
2
7.69%
题型统计
大题类型
数量
占比
选择题
12
46.15%
填空题
5
19.23%
解答题
9
34.61%
知识点统计
知识点
数量
占比
有理数的乘除法
1
3.84%
勾股定理
1
3.84%
有理数
1
3.84%
图形的相似
1
3.84%
课题学习 最短路径问题
1
3.84%
平面直角坐标系
1
3.84%
实际问题与二元一次方程组
1
3.84%
等腰三角形
2
7.69%
解直角三角形与其应用
1
3.84%
分式方程
1
3.84%
反比例函数
1
3.84%
二次根式的加减
1
3.84%
整式
1
3.84%
弧长和扇形面积
1
3.84%
一次函数
2
7.69%
实际问题与一元一次方程
1
3.84%
二元一次方程组
1
3.84%
乘法公式
1
3.84%
平行四边形
1
3.84%
直方图
1
3.84%
有理数的加减法
1
3.84%
实际问题与一元二次方程
1
3.84%
二次函数单元测试
1
3.84%
三角形全等的判定
1
3.84%
版权提示
该作品由: 用户庄月昊分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。