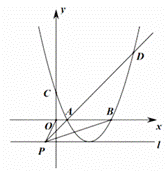
如图所示,二次函数![]() 的图像(记为抛物线
的图像(记为抛物线![]() )与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为
)与y轴交于点C,与x轴分别交于点A、B,点A、B的横坐标分别记为![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() ,
,![]() ,且过点
,且过点![]() ,求该二次函数的表达式;
,求该二次函数的表达式;
(2)若关于x的一元二次方程![]() 的判别式
的判别式![]() .求证:当
.求证:当![]() 时,二次函数
时,二次函数![]() 的图像与x轴没有交点.
的图像与x轴没有交点.
(3)若![]() ,点P的坐标为
,点P的坐标为![]() ,过点P作直线l垂直于y轴,且抛物线的
,过点P作直线l垂直于y轴,且抛物线的![]() 顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线
顶点在直线l上,连接OP、AP、BP,PA的延长线与抛物线![]() 交于点D,若
交于点D,若![]() ,求
,求![]() 的最小值.
的最小值.
(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)根据题意,把![]() ,
,![]() ,点
,点![]() ,代入解析式,即可求出解析式;
,代入解析式,即可求出解析式;
(2)利用根的判别式进行判断,即可得到结论;
(3)根据二次函数的性质,得到![]() ,结合根与系数的关系,得到
,结合根与系数的关系,得到![]() ,然后证明
,然后证明![]() ,得到
,得到![]() ,然后得到
,然后得到![]() ,利用二次根式的性质即可得到答案.
,利用二次根式的性质即可得到答案.
【详解】
解:(1)由题意得:![]() ,
,
∵函数过点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)由题意,一元二次方程![]() 的判别式
的判别式![]() .
.
∴![]() ,
,
∴![]() ,
,
在函数![]() 中,
中,
![]()
∵![]() ,
,
∴![]() ,
,
即函数图象与x轴没有交点.
(3)因为函数顶点在直线l上,则有![]() ,
,
即![]() ①
①
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
由①得:![]() ②
②
∵![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]() ,
,
则![]() .
.
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
由②得:![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() .
.
【点睛】
本题考查了二次函数的综合问题,相似三角形的判定和性质,一元二次方程根的判别式,根与系数的关系,解题的关键是熟练掌握相似三角形的判定和性质,二次函数的最值等知识进行解题.
如图所示,![]() 的顶点A在反比例函数
的顶点A在反比例函数![]() 的图像上,直线AB交y轴于点C,且点C的纵坐标为5,过点A、B分别作y轴的垂线AE、BF,垂足分别为点E、F,且
的图像上,直线AB交y轴于点C,且点C的纵坐标为5,过点A、B分别作y轴的垂线AE、BF,垂足分别为点E、F,且![]() .
.
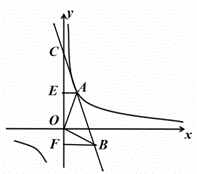
(1)若点E为线段OC的中点,求k的值;
(2)若![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,其面积小于3.
,其面积小于3.
①求证:![]() ;
;
②把![]() 称为
称为![]() ,
,![]() 两点间的“ZJ距离”,记为
两点间的“ZJ距离”,记为![]() ,求
,求![]() 的值.
的值.
(1)![]() ;(2)①见解析;②8.
;(2)①见解析;②8.
【解析】
(1)由点E为线段OC的中点,可得E点坐标为![]() ,进而可知A点坐标为:
,进而可知A点坐标为:![]() ,代入解析式即可求出k;
,代入解析式即可求出k;
(2)①由![]() 为等腰直角三角形,可得
为等腰直角三角形,可得![]() ,再根据同角的余角相等可证
,再根据同角的余角相等可证![]() ,由AAS即可证明
,由AAS即可证明![]() ;
;
②由“ZJ距离”的定义可知![]() 为MN两点的水平距离与垂直距离之和,故
为MN两点的水平距离与垂直距离之和,故![]() ,即只需求出B点坐标即可,设点
,即只需求出B点坐标即可,设点![]() ,由
,由![]() 可得
可得![]() ,进而代入直线AB解析式求出k值即可解答.
,进而代入直线AB解析式求出k值即可解答.
【详解】
解:(1)∵点E为线段OC的中点,OC=5,
∴![]() ,即:E点坐标为
,即:E点坐标为![]() ,
,
又∵AE⊥y轴,AE=1,
∴![]() ,
,
∴![]() .
.
(2)①在![]() 为等腰直角三角形中,
为等腰直角三角形中,![]() ,
,![]() ,
,
∴![]() ,
,
又∵BF⊥y轴,
∴![]() ,
,
∴![]()
在![]() 和
和![]() 中
中
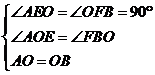 ,
,
∴![]() ,
,
②解:设点![]() 坐标为
坐标为![]() ,
,
∵![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
设直线AB解析式为:![]() ,将AB两点代入得:
,将AB两点代入得:
则![]() .
.
解得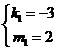 ,
,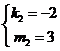 .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,符合;
,符合;
∴![]()
![]()
![]()
![]()
![]()
![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,不符,舍去;
,不符,舍去;
综上所述:![]() .
.
【点睛】
此题属于代几综合题,涉及的知识有:反比例函数、一次函数的性质及求法、三角形全等的判定及性质、等腰直角三角形性质等,熟练掌握三角形全等的性质和判定和数形结合的思想是解本题的关键.
AB是![]() 的直径,点C是
的直径,点C是![]() 上一点,连接AC、BC,直线MN过点C,满足
上一点,连接AC、BC,直线MN过点C,满足![]() .
.
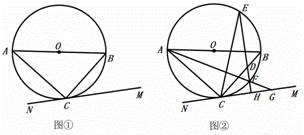
(1)如图①,求证:直线MN是![]() 的切线;
的切线;
(2)如图②,点D在线段BC上,过点D作![]() 于点H,直线DH交
于点H,直线DH交![]() 于点E、F,连接AF并延长交直线MN于点G,连接CE,且
于点E、F,连接AF并延长交直线MN于点G,连接CE,且![]() ,若
,若![]() 的半径为1,
的半径为1,![]() ,求
,求![]() 的值.
的值.
(1)见解析 (2)![]()
【解析】
(1)由圆周角定理的推论和直角三角形的性质可得![]() ,由
,由![]() 可得
可得![]() ,进一步即可推出
,进一步即可推出![]() ,从而可得结论;
,从而可得结论;
(2)如图②,由已知条件易求出AC的长,根据对顶角相等和圆周角定理可得∠1=∠3,根据余角的性质可得![]() ,进而可得
,进而可得![]() ∽
∽![]() ,于是根据相似三角形的性质变形可得
,于是根据相似三角形的性质变形可得![]() ,进一步即可求出结果.
,进一步即可求出结果.
【详解】
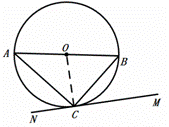
解:(1)证明:连接OC,如图,
∵AB是![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴MN是![]() 的切线;
的切线;
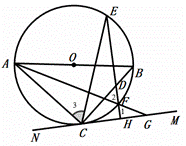
(2)如图②,∵![]() ,即
,即![]() ,∴
,∴![]() ,
,
∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∵![]() ,2
,2
∴∠1+∠AGC=90°,
∵∠3+∠ECD=90°,
∴![]() ,
,
又∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() .
.
【点睛】
本题考查了圆的切线的判定、等腰三角形的性质、解直角三角形、圆周角定理的推论以及相似三角形的判定和性质等知识,属于常考题型,熟练掌握上述知识、灵活应用相似三角形的判定和性质是解题的关键.
如图所示,![]() 的顶点E在正方形ABCD对角线AC的延长线上,AE与BF交于点G,连接AF、CF,满足
的顶点E在正方形ABCD对角线AC的延长线上,AE与BF交于点G,连接AF、CF,满足![]() .
.
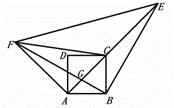
(1)求证:![]() .
.
(2)若正方形ABCD的边长为1,![]() ,求
,求![]() 的值.
的值.
(1)见解析;(2)![]()
【解析】
(1)已知![]() ,根据全等三角形的对应角相等可得
,根据全等三角形的对应角相等可得![]() ,再由
,再由![]() ,可得
,可得![]() ,即可证得
,即可证得![]() ;(2)由
;(2)由![]() ,根据全等三角形的对应角相等可得
,根据全等三角形的对应角相等可得![]() ,由对顶角相等可得
,由对顶角相等可得![]() ,即可证得
,即可证得![]() ;又因正方形边长为1,
;又因正方形边长为1,![]() ,可得
,可得![]() ,
,![]() .在Rt△AFC中,即可求得
.在Rt△AFC中,即可求得![]() .
.
【详解】
(1)证明:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵正方形边长为1,![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
【点睛】
本题考查了全等三角形的性质、正方形的性质及锐角三角函数的知识,熟练运用相关知识是解决问题的关键.
近几年,国内快递业务快速发展,由于其便捷、高效,人们越来越多地通过快递公司代办点来代寄包裹.某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据(每天代寄包裹数、天数均为整数)统计如下:

(1)求该数据中每天代寄包裹数在![]() 范围内的天数;
范围内的天数;
(2)若该代办点对顾客代寄包裹的收费标准为:重量小于或等于1千克的包裹收费8元;重量超1千克的包裹,在收费8元的基础上,每超过1千克(不足1千克的按1千克计算)需再收取2元.
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包表中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
| 重量G(单位:千克) |
|
|
|
| 件数(单位:件) | 15 | 10 | 15 |
求这40件包裹收取费用的平均数.
(1)42天;(2)①10元; ②14
【解析】
(1)根据统计图读出50.5~100.5的天数,100.5~150.5的天数,150.5~200.5的天数,再将三个数据相加即可;
(2)①应付费用等于基础费用加上超过部分的费用;
②求加权平均数即可.
【详解】
解:(1)结合统计图可知:每天代寄包裹数在50.5~200.5范围内的天数为18+12+12=42天;
(2)①因为1.6>1,故重量超过了1kg,除了付基础费用8元,还需要付超过1k部分0.6kg的费用2元,
则该顾客应付费用为8+2=10元;
②![]() 元.
元.
所以这40件包裹收取费用的平均数为14元.
【点睛】
本题考查频数分布直方图、加权平均数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
本卷还有21题,登录并加入会员即可免费使用哦~

该作品由: 用户吴思思分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。