已知函数![]() 均为一次函数,m为常数.
均为一次函数,m为常数.
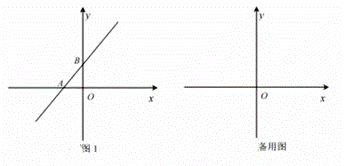
(1)如图1,将直线![]() 绕点
绕点![]() 逆时针旋转45°得到直线
逆时针旋转45°得到直线![]() ,直线
,直线![]() 交y轴于点B.若直线
交y轴于点B.若直线![]() 恰好是
恰好是![]() 中某个函数的图象,请直接写出点B坐标以及m可能的值;
中某个函数的图象,请直接写出点B坐标以及m可能的值;
(2)若存在实数b,使得![]() 成立,求函数
成立,求函数![]() 图象间的距离;
图象间的距离;
(3)当![]() 时,函数
时,函数![]() 图象分别交x轴,y轴于C,E两点,
图象分别交x轴,y轴于C,E两点,![]() 图象交x轴于D点,将函数
图象交x轴于D点,将函数![]() 的图象最低点F向上平移
的图象最低点F向上平移![]() 个单位后刚好落在一次函数
个单位后刚好落在一次函数![]() 图象上,设
图象上,设![]() 的图象,线段
的图象,线段![]() ,线段
,线段![]() 围成的图形面积为S,试利用初中知识,探究S的一个近似取值范围.(要求:说出一种得到S的更精确的近似值的探究办法,写出探究过程,得出探究结果,结果的取值范围两端的数值差不超过0.01.)
围成的图形面积为S,试利用初中知识,探究S的一个近似取值范围.(要求:说出一种得到S的更精确的近似值的探究办法,写出探究过程,得出探究结果,结果的取值范围两端的数值差不超过0.01.)
(1)(0,1);1或0 (2)![]() (3)
(3)![]()
【解析】
(1)由题意,可得点B坐标,进而求得直线![]() 的解析式,再分情况讨论即可解的m值;
的解析式,再分情况讨论即可解的m值;
(2)由非负性解得m和b的值,进而得到两个函数解析式,设![]() 与x轴、y轴交于T,P,
与x轴、y轴交于T,P,![]() 分别与x轴、y轴交于G,H,连接GP,TH,证得四边形GPTH是正方形,求出GP即为距离;
分别与x轴、y轴交于G,H,连接GP,TH,证得四边形GPTH是正方形,求出GP即为距离;
(3)先根据解析式,用m表示出点C、E、D的坐标以及y关于x的表达式为![]() ,得知y是关于x的二次函数且开口向上、最低点为其顶点
,得知y是关于x的二次函数且开口向上、最低点为其顶点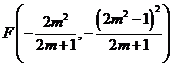 ,根据坐标平移规则,得到关于m的方程,解出m值,即可得知点D 、E的坐标且抛物线过D、E点,观察图象,即可得出S的大体范围,如:
,根据坐标平移规则,得到关于m的方程,解出m值,即可得知点D 、E的坐标且抛物线过D、E点,观察图象,即可得出S的大体范围,如:![]() ,较小的可为平行于DE且与抛物线相切时围成的图形面积.
,较小的可为平行于DE且与抛物线相切时围成的图形面积.
【详解】
解:(1)由题意可得点B坐标为(0,1),
设直线![]() 的表达式为y=kx+1,将点A(-1,0)代入得:k=1,
的表达式为y=kx+1,将点A(-1,0)代入得:k=1,
所以直线![]() 的表达式为:y=x+1,
的表达式为:y=x+1,
若直线![]() 恰好是
恰好是![]() 的图象,则2m-1=1,解得:m=1,
的图象,则2m-1=1,解得:m=1,
若直线![]() 恰好是
恰好是![]() 的图象,则2m+1=1,解得:m=0,
的图象,则2m+1=1,解得:m=0,
综上,![]() ,
,![]() 或者
或者![]()
(2)如图,![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
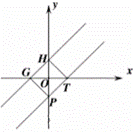
设![]() 与x轴、y轴交于T,P,
与x轴、y轴交于T,P,![]() 分别与x轴、y轴交于G,H,连接GP,TH
分别与x轴、y轴交于G,H,连接GP,TH
![]() ,
,![]()
![]() 四边形GPTH是正方形
四边形GPTH是正方形
![]() ,
,![]() ,即
,即![]()
![]()
![]() ;
;
(3)![]() ,
,![]()
![]() 分别交x轴,y轴于C,E两点
分别交x轴,y轴于C,E两点
![]() ,
,![]()
![]() 图象交x轴于D点
图象交x轴于D点
![]()
![]()
![]()
![]()
![]() 二次函数
二次函数![]() 开口向上,它的图象最低点在顶点
开口向上,它的图象最低点在顶点
![]() 顶点
顶点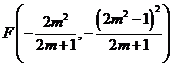
![]() 抛物线顶点F向上平移
抛物线顶点F向上平移![]() ,刚好在一次函数
,刚好在一次函数![]() 图象上
图象上
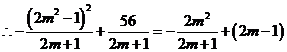 且
且![]()
![]()
![]() ,
,
∴![]() ,
,![]()
![]() 由
由![]() ,
,![]() 得到
得到![]() ,
,![]() ,
,
由![]() 得到与x轴,y轴交点是
得到与x轴,y轴交点是![]() ,
,![]() ,
,![]() ,
,
![]() 抛物线经过
抛物线经过![]() ,
,![]() 两点
两点
![]() 的图象,线段OD,线段OE围成的图形是封闭图形,则S即为该封闭图形的面积
的图象,线段OD,线段OE围成的图形是封闭图形,则S即为该封闭图形的面积
探究办法:利用规则图形面积来估算不规则图形的面积.
探究过程:
①观察大于S的情况.
很容易发现![]()
![]() ,
,![]()
![]()
(若有S小于其他值情况,只要合理,参照赋分.)
②观察小于S的情况.
选取小于S的几个特殊值来估计更精确的S的近似值,取值会因人而不同,下面推荐一种方法,选取以下三种特殊位置:
位置一:如图
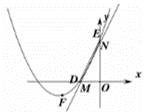
当直线MN与DE平行且与抛物线有唯一交点时,设直线MN与x,y轴分别交于M,N
![]() ,
,![]()
![]() 直线
直线![]()
设直线![]()
![]()
![]()
![]() ,
,![]()
![]() 直线
直线![]()
![]() 点
点![]()
![]()
位置二:如图

当直线DR与抛物线有唯一交点时,直线DR与y轴交于点R
设直线![]() ,
,![]()
![]() 直线
直线![]()
![]()
![]()
![]() ,
,![]()
![]() 直线
直线![]()
![]() 点
点![]()
![]()
位置三:如图
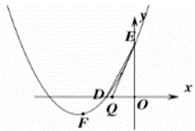
当直线EQ与抛物线有唯一交点时,直线EQ与x轴交于点Q
设直线![]()
![]()
![]()
![]() ,
,![]()
![]() 直线
直线![]()
![]() 点
点![]()
![]()
![]()
我们发现:在曲线DE两端位置时的三角形的面积远离S的值,由此估计在曲线DE靠近中间部分时取值越接近S的值
探究的结论:按上述方法可得一个取值范围![]()
(备注:不同的探究方法会有不同的结论,因而会有不同的答案.只要来龙去脉清晰、合理,即可参照赋分,但若直接写出一个范围或者范围两端数值的差不在0.01之间不得分.)
【点睛】
本题是一道综合性很强的代数与几何相结合的压轴题,知识面广,涉及有旋转的性质、坐标平移规则、非负数的性质、一次函数的图象与性质、二次函数的图象与性质、一元二次方程、不规则图形面积的估计等知识,解答的关键是认真审题,找出相关信息,利用待定系数法、数形结合法等解题方法确定解题思路,利用相关信息进行推理、探究、发现和计算.
菱形![]() 的对角线
的对角线![]() 相交于点O,
相交于点O,![]() ,点G是射线
,点G是射线![]() 上一个动点,过点G作
上一个动点,过点G作![]() 交射线
交射线![]() 于点E,以
于点E,以![]() 为邻边作矩形
为邻边作矩形![]() .
.
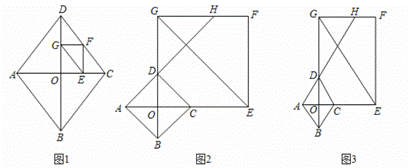
(1)如图1,当点F在线段![]() 上时,求证:
上时,求证:![]() ;
;
(2)若延长![]() 与边
与边![]() 交于点H,将
交于点H,将![]() 沿直线
沿直线![]() 翻折180°得到
翻折180°得到![]() .
.
①如图2,当点M在![]() 上时,求证:四边形
上时,求证:四边形![]() 为正方形:
为正方形:
②如图3,当![]() 为定值
为定值![]() 时,设
时,设![]() ,k为大于0的常数,当且仅当
,k为大于0的常数,当且仅当![]() 时,点M在矩形
时,点M在矩形![]() 的外部,求m的值.
的外部,求m的值.
(1)见解析;(2)①见解析;②![]() .
.
【解析】
(1)证明四边形ECFG,DGEF是平行四边形即可得到结论;
(2)①由折叠得![]() 可证明
可证明![]() ,
,![]() ,再证明
,再证明![]() 可得GO=EO,再由四边形EOGF为矩形则可证明结论;
可得GO=EO,再由四边形EOGF为矩形则可证明结论;
②由四边形ABCD为菱形以及折叠可得![]() ,当且仅当
,当且仅当![]() 时,M点在矩形EOGF的外部,
时,M点在矩形EOGF的外部,![]() 时,M点在矩形EOGF上,即点M在EF上,设
时,M点在矩形EOGF上,即点M在EF上,设![]() ,求得
,求得![]() ,过点D作
,过点D作![]() 于点N,证明
于点N,证明![]() 求得
求得![]() ,在
,在![]() 中运用勾股定理列出方程
中运用勾股定理列出方程![]() 求解即可.
求解即可.
【详解】
(1)证明:如图,![]() 四边形EOGF为矩形,
四边形EOGF为矩形,
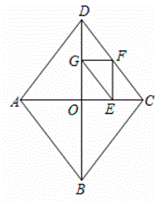
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形ECFG,DGEF是平行四边形,
四边形ECFG,DGEF是平行四边形,
![]() ,
,![]() ,
,
![]() ;
;
(2)如图,
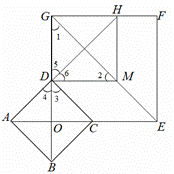
证明:由折叠得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形ABCD为菱形,
四边形ABCD为菱形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,点M在GE上,
,点M在GE上,
![]() ,
,
![]() ,
,
![]() 四边形EOGF为矩形,
四边形EOGF为矩形,
![]() 矩形EOGF为正方形;
矩形EOGF为正方形;
(3)如图,
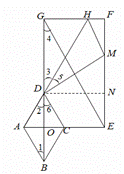
![]() 四边形ABCD为菱形,
四边形ABCD为菱形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (m为定值),
(m为定值),
![]() ,
,
![]() 点M始终在固定射线DM上并随k的增大向上运动,
点M始终在固定射线DM上并随k的增大向上运动,
![]() 当且仅当
当且仅当![]() 时,M点在矩形EOGF的外部,
时,M点在矩形EOGF的外部,
![]() 时,M点在矩形EOGF上,即点M在EF上,
时,M点在矩形EOGF上,即点M在EF上,
设![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
过点D作![]() 于点N,
于点N,
![]() ,又
,又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是直角三角形,
是直角三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (负值舍去),
(负值舍去),
![]() ,
,
![]() .
.
【点睛】
本题考查四边形的综合问题,涉及矩形和菱形的性质,勾股定理,锐角三角函数,解方程等知识,综合程度较高,考查学生灵活运用知识的能力.
资料:公司营销区域面积是指公司营销活动范围内的地方面积,公共营销区域面积是指两家及以上公司营销活动重叠范围内的地方面积.
材料:某地有A,B两家商贸公司(以下简称A,B公司).去年下半年A,B公司营销区域面积分别为m平方千米,n平方千米,其中![]() ,公共营销区域面积与A公司营销区域面积的比为
,公共营销区域面积与A公司营销区域面积的比为![]() ;今年上半年,受政策鼓励,各公司决策调整,A公司营销区域面积比去年下半年增长了
;今年上半年,受政策鼓励,各公司决策调整,A公司营销区域面积比去年下半年增长了![]() ,B公司营销区域面积比去年下半年增长的百分数是A公司的4倍,公共营销区域面积与A公司营销区域面积的比为
,B公司营销区域面积比去年下半年增长的百分数是A公司的4倍,公共营销区域面积与A公司营销区域面积的比为![]() ,同时公共营销区域面积与A,B两公司总营销区域面积的比比去年下半年增加了x个百分点.
,同时公共营销区域面积与A,B两公司总营销区域面积的比比去年下半年增加了x个百分点.
问题:(1)根据上述材料,针对去年下半年,提出一个你喜欢的数学问题(如求去年下半年公共营销区域面积与B公司营销区域面积的比),并解答;
(2)若同一个公司去年下半年和今年上半年每平方千米产生的经济收益持平,且A公司每半年每平方千米产生的经济收益均为B公司的1.5倍,求去年下半年与今年上半年两公司总经济收益之比.
(1)见解析;(2)55:72
【解析】
(1)根据题意任意写出问题解答即可.
(2)根据题意列出等式,解出增长率再代入A,B的收益中计算即可.
【详解】
解(1)问题1:求去年下半年公共营销区域面积与B公司营销区域面积的比
解答:![]()
![]()
问题2:A公司营销区域面积比B公司营销区域的面积多多少?
解答:![]()
问题3:求去年下半年公共营销区域面积与两个公司总营销区域面积的比
解答:![]()
![]()
(2)方法一:

方法二:
![]()
方法三:
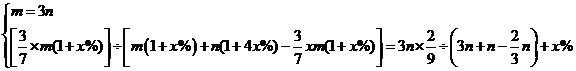
![]() 解得
解得![]() ,
,![]() (舍去)
(舍去)
设B公司每半年每平方千米产生的经济收益为a,则A公司每半年每平方千米产生的经济收益为![]()
今年上半年A,B公司产生的总经济收益为![]()
去年下半年A,B公司产生的总经济收益为![]()
去年下半年与今年上半年两公司总经济收益之比为![]()
【点睛】
本题考查一元二次方程增长率的问题,关键在于理解题意列出等式方程.
如图,在四边形![]() 中,
中,![]() ,过点B的
,过点B的![]() 与边
与边![]() 分别交于E,F两点.
分别交于E,F两点.![]() ,垂足为G,
,垂足为G,![]() .连接
.连接![]() .
.
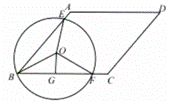
(1)若![]() ,试判断
,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)若![]() ,求证:
,求证:![]() 与
与![]() 相切于点A.
相切于点A.
(1)等腰直角三角形,理由见解析 (2)见解析
【解析】
(1)根据题目中已知信息,可知![]() ,有
,有![]() ,所以
,所以![]() ,
,![]() 都是等腰直角三角形,得到
都是等腰直角三角形,得到![]() ,
,![]() 即可得出
即可得出![]() 是等腰直角三角形;
是等腰直角三角形;
(2)通过![]() ,可以等到
,可以等到![]() ,有
,有![]() ,又因为
,又因为![]() ,可以知道E与点A重合,再证明
,可以知道E与点A重合,再证明![]() 即可.
即可.
【详解】
解:(1)![]() 是等腰直角三角形
是等腰直角三角形
理由如下:
∵![]()
∴![]()
∵![]()
∴![]()
∴![]() ,
,![]() 都是等腰直角三角形
都是等腰直角三角形
∴![]()
∴![]()
∵![]()
∴![]() 是等腰直角三角形
是等腰直角三角形
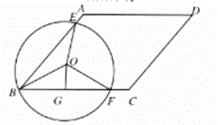
(2)证明:![]()
∴![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴点E与点A重合
以下有多种方法:
方法一∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() 是
是![]() 的半径
的半径
∴![]() 与
与![]() 相切于点A
相切于点A
方法二∵![]() ,∴
,∴![]()
∴![]()
又![]()
∴![]()
∴G,A,O三点共线
∵![]()
∴![]()
∴![]() 与
与![]() 相切于点A.
相切于点A.
方法三:如图
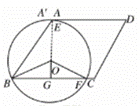
∵![]()
∴![]() 与
与![]() 之间距离:
之间距离:![]()
延长![]() 交
交![]() 的延长线交于点
的延长线交于点![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]() ,
,![]()
∴![]() 与
与![]() 相切于点
相切于点![]()
又![]()
∴点![]() 与点
与点![]() 重合
重合
∴![]() 与
与![]() 相切于点
相切于点![]() .
.
【点睛】
(1)证明三角形形状需要找到边的关系以及角的大小,通过题目中的已知信息先判断出特殊三角形,再找到所求三角形与特殊三角形边与角的关系是解题的关键;
(2)本题主要考查了全等三角形的性质以及如何求切线,通过三角形全等得到角的大小,从而可以证明点E与点A重合,再证明![]() 即可得
即可得![]() 与
与![]() 相切于点
相切于点![]() ,其中证明点E与点A重合是解题的关键.
,其中证明点E与点A重合是解题的关键.
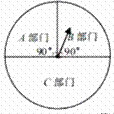
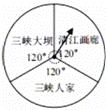
宜昌景色宜人,其中三峡大坝、清江画廊、三峡人家景点的景色更是美不胜收.某民营单位为兼顾生产和业余生活,决定在下设的A,B,C三部门利用转盘游戏确定参观的景点,两转盘各部分圆心角大小以及选派部门、旅游景点等信息如图.
(1)若规定老同志相对偏多的部门选中的可能性大,试判断这个部门是哪个部门?请说明理由;
(2)设选中C部门游三峡大坝的概率为![]() ,选中B部门游清江画廊或者三峡人家的概率为
,选中B部门游清江画廊或者三峡人家的概率为![]() ,请判断
,请判断![]() ,
,![]() 大小关系,并说明理由.
大小关系,并说明理由.
(1)C部门,理由见解析;(2)P1=P2,理由见解析
【解析】
(1)利用圆心角为360°,A,B,C分别占90°,90°和180°,分别求出所占百分比即可;
(2)列出所有可能的情况,然后得出C,B所占比例,即可得出结果.
【详解】
解:(1)C部门,
理由:∵![]()
![]()
(2)![]() ,
,
理由:
| A | B |
|
| |
| 三峡大坝(D) |
|
|
|
|
| 清江画廊(E) |
|
|
|
|
| 三峡人家(F) |
|
|
|
|
备注:部门转盘平均分成了4等份,C部门占两份分别用![]() ,
,![]() 表示
表示
由表可得,所有可能出现的结果共有12种,这些结果出现的可能性相等,其中C选中三峡大坝的结果有2种,B选中清江画廊或者三峡人家的结果有2种
∴![]()
![]()
∴![]()
【点睛】
本题考查了扇形图的知识.用到的知识点为:概率=所求情况数与总情况数之比.关键是分析扇形图,得到相关的数据信息.
本卷还有19题,登录并加入会员即可免费使用哦~

该作品由: 用户阳光之舟分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。