2020四川人教版初中数学中考模拟137566
初中
整体难度：中等
2020-09-14
题号
一
二
三
四
五
评分
一、解答题 (共8题)
添加该题型下试题
1.
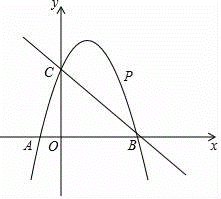
（2019·江苏中考模拟）如图，已知二次函数y=ax2+2x+c的图象经过点C（0，3），与x轴分别交于点A，点B（3，0）．点P是直线BC上方的抛物线上一动点．
（1）求二次函数y=ax2+2x+c的表达式；
（2）连接PO，PC，并把△POC沿y轴翻折，得到四边形POP′C．若四边形POP′C为菱形，请求出此时点P的坐标；
（3）当点P运动到什么位置时，四边形ACPB的面积最大？求出此时P点的坐标和四边形ACPB的最大面积．
难度：
知识点：二次函数与一元二次方程
使用次数：172
【答案】
（1）y=﹣x2+2x+3（2）（
，
）（3）当点P的坐标为（，
）时，四边形ACPB的最大面积值为
【解析】
（1）将点B和点C的坐标代入函数解析式，得
解得
二次函数的解析式为y=﹣x2+2x+3；
（2）若四边形POP′C为菱形，则点P在线段CO的垂直平分线上，
如图1，连接PP′，则PE⊥CO，垂足为E，
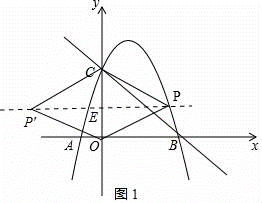
∵C（0，3），
∴
∴点P的纵坐标，
当
时，即
解得
（不合题意，舍），
∴点P的坐标为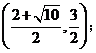
（3）如图2，
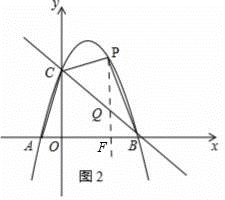
P在抛物线上，设P（m，﹣m2+2m+3），
设直线BC的解析式为y=kx+b，
将点B和点C的坐标代入函数解析式，得
解得
直线BC的解析为y=﹣x+3，
设点Q的坐标为（m，﹣m+3），
PQ=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m．
当y=0时，﹣x2+2x+3=0，
解得x1=﹣1，x2=3，
OA=1，
S四边形ABPC=S△ABC+S△PCQ+S△PBQ
当m=时，四边形ABPC的面积最大．
当m=时，
，即P点的坐标为
当点P的坐标为
时，四边形ACPB的最大面积值为．
【点睛】
本题考查了二次函数综合题，解（1）的关键是待定系数法；解（2）的关键是利用菱形的性质得出P点的纵坐标，又利用了自变量与函数值的对应关系；解（3）的关键是利用面积的和差得出二次函数，又利用了二次函数的性质．
2.
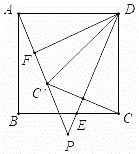
（2019·北京中考模拟）如图，在正方形ABCD中，E是边BC上的一动点（不与点B、C重合），连接DE、点C关于直线DE的对称点为C′，连接AC′并延长交直线DE于点P，F是AC′的中点，连接DF．
（1）求∠FDP的度数；
（2）连接BP，请用等式表示AP、BP、DP三条线段之间的数量关系，并证明；
（3）连接AC，若正方形的边长为
，请直接写出△ACC′的面积最大值．
难度：
知识点：特殊的平行四边形
使用次数：126
【答案】
（1）45°；（2）BP+DP＝AP，证明详见解析；（3）﹣1．
【解析】
（1）由对称得：CD＝C'D，∠CDE＝∠C'DE，
在正方形ABCD中，AD＝CD，∠ADC＝90°，
∴AD＝C'D，
∵F是AC'的中点，
∴DF⊥AC'，∠ADF＝∠C'DF，
∴∠FDP＝∠FDC'+∠EDC'＝
∠ADC＝45°；
（2）结论：BP+DP＝AP，
理由是：如图，作AP'⊥AP交PD的延长线于P'，
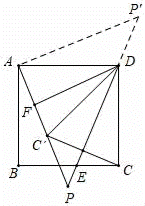
∴∠PAP'＝90°，
在正方形ABCD中，DA＝BA，∠BAD＝90°，
∴∠DAP'＝∠BAP，
由（1）可知：∠FDP＝45°
∵∠DFP＝90°
∴∠APD＝45°，
∴∠P'＝45°，
∴AP＝AP'，
在△BAP和△DAP'中，
∵
，
∴△BAP≌△DAP'（SAS），
∴BP＝DP'，
∴DP+BP＝PP'＝AP；
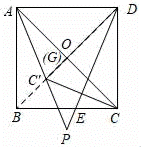
（3）如图，过C'作C'G⊥AC于G，则S△AC'C＝AC•C'G，
Rt△ABC中，AB＝BC＝，
∴AC＝
，即AC为定值，
当C'G最大值，△AC'C的面积最大，
连接BD，交AC于O，当C'在BD上时，C'G最大，此时G与O重合，
∵CD＝C'D＝，OD＝AC＝1，
∴C'G＝﹣1，
∴S△AC'C＝
．
【点睛】
本题考查四边形综合题、正方形的性质、等腰直角三角形的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．
3.
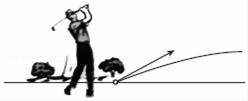
（2019·四川中考模拟）如图，以40m/s的速度将小球沿与地面成30°角的方向击出时，小球的飞行路线是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系h＝20t﹣5t2．
（1）小球飞行时间是多少时，小球最高？最大高度是多少？
（2）小球飞行时间t在什么范围时，飞行高度不低于15m？
难度：
知识点：实际问题与二次函数
使用次数：163
【答案】
（1）小球飞行时间是2s时，小球最高为20m；(2) 1≤t≤3.
【解析】
（1）∵h＝﹣5t2+20t＝﹣5（t﹣2）2+20，
∴当t＝2时，h取得最大值20米；
答：小球飞行时间是2s时，小球最高为20m；
（2）如图，
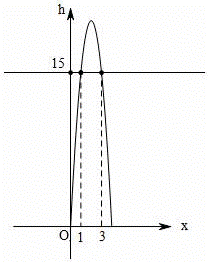
由题意得：15＝20t﹣5t2，
解得：t1＝1，t2＝3，
由图象得：当1≤t≤3时，h≥15，
则小球飞行时间1≤t≤3时，飞行高度不低于15m．
【点睛】
本题考查了二次函数的应用，主要考查了二次函数的最值问题，以及利用二次函数图象求不等式，并熟练掌握二次函数的性质是解题的关键．
4.
2019·山东中考模拟）如图，⊙O的直径AB的长为2，点C在圆周上，∠CAB=30°，点D是圆上一动点，DE∥AB交CA的延长线于点E，连接CD，交AB于点F．
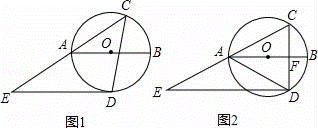
（Ⅰ）如图1，当∠ACD=45°时，请你判断DE与⊙O的位置关系并加以证明；
（Ⅱ）如图2，当点F是CD的中点时，求△CDE的面积．
难度：
知识点：点和圆、直线和圆的位置关系
使用次数：173
【答案】
（Ⅰ）DE与⊙O相切（2）
【解析】
（1）如图1中，连接OD．
∵∠C=45°，
∴∠AOD=2∠C=90°，
∵ED∥AB，
∴∠AOD+∠EDO=180°，
∴∠EDO=90°，
∴ED⊥OD，
∴ED是⊙O切线．
（2）如图2中，连接BC，
∵CF=DF，
∴AF⊥CD，
∴AC=AD，
∴∠ACD=∠ADC，
∵AB∥ED，
∴ED⊥DC，
∴∠EDC=90°，
在RT△ACB中，∵∠ACB=90°，∠CAB=30°，AB=2，
∴BC=1，AC=
，
∴CF=
AC=
，CD=2CF=，
在RT△ECD中，
∵∠EDC=90°，CD=，∠E=∠CAB=30°，
∴EC=2CD=2，ED=
=3，
∴S△ECD=•ED•CD=
．
考点：切线的判定．
5.
（2019·山东中考模拟）如图，A（4，3）是反比例函数y=
在第一象限图象上一点，连接OA，过A作AB∥x轴，截取AB=OA（B在A右侧），连接OB，交反比例函数y=的图象于点P．
（1）求反比例函数y=的表达式；
（2）求点B的坐标；
（3）求△OAP的面积．
难度：
知识点：反比例函数
使用次数：181
【答案】
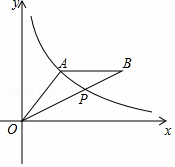
（1）反比例函数解析式为y=
；（2）点B的坐标为（9，3）；（3）△OAP的面积=5．
【解析】
（1）将点A（4，3）代入y=，得：k=12，
则反比例函数解析式为y=；
（2）如图，过点A作AC⊥x轴于点C，
则OC=4、AC=3，
∴OA=
=5，
∵AB∥x轴，且AB=OA=5，
∴点B的坐标为（9，3）；
（3）∵点B坐标为（9，3），
∴OB所在直线解析式为y=
x，
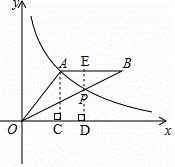
由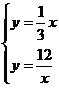
可得点P坐标为（6，2），（负值舍去），
过点P作PD⊥x轴，延长DP交AB于点E，
则点E坐标为（6，3），
∴AE=2、PE=1、PD=2，
则△OAP的面积=×（2+6）×3﹣×6×2﹣×2×1=5．
【点睛】本题考查了反比例函数与几何图形综合，熟练掌握反比例函数图象上点的坐标特征、正确添加辅助线是解题的关键.
本卷还有24题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
29
总体难度：
中等
难度统计
难度系数
数量
占比
中等
5
17.24%
容易
24
82.75%
题型统计
大题类型
数量
占比
解答题
8
27.58%
填空题
9
31.03%
计算题
2
6.89%
选择题
10
34.48%
知识点统计
知识点
数量
占比
二次函数与一元二次方程
2
6.89%
特殊的平行四边形
2
6.89%
实际问题与二次函数
1
3.44%
反比例函数
2
6.89%
相似三角形
2
6.89%
一次函数
2
6.89%
解一元二次方程
1
3.44%
分式方程
2
6.89%
点和圆、直线和圆的位置关系
2
6.89%
统计调查
2
6.89%
分式的运算
1
3.44%
锐角三角函数
1
3.44%
与三角形有关的角
1
3.44%
因式分解
1
3.44%
实际问题与一元二次方程
1
3.44%
平面直角坐标系
1
3.44%
平行线的性质
1
3.44%
几何图形
1
3.44%
有理数的乘方
1
3.44%
（补充）整式的除法
1
3.44%
有理数
1
3.44%
版权提示
该作品由: 用户郑丹分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。