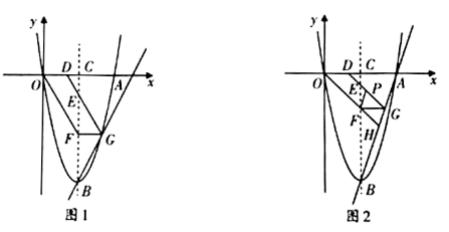
如图,已知抛物线![]() 经过点A(6,0),顶点为B,对称轴BC交x轴于点C.点D的坐标为(2,0),点E是在x轴下方的抛物线对称轴上的一个动点,OF//DE交 BC于点F,FG//x轴交射线 DE于点G,作直线BG.
经过点A(6,0),顶点为B,对称轴BC交x轴于点C.点D的坐标为(2,0),点E是在x轴下方的抛物线对称轴上的一个动点,OF//DE交 BC于点F,FG//x轴交射线 DE于点G,作直线BG.
(1)求点B的坐标:
(2)如图1,当点G恰好落在该抛物线上时,求点E的坐标;
(3)如图2,当CE=1时,判断点A是否在直线BG上,说明理由;
(4)在(3)的条件下,延长OF交BG于点H,取DG中点P,连接PF,探究四边形PFHG是否为平行四边形,并说明理由
考点:二次函数综合:与平行四边形的构造
答案:(1) B(3,-9);(2) E(3,![]() )
)
(3)点A在直线BG上;
(4 )四边形PFHG是平行四边形.
解析:( 1 )将点A4(6,0)代入![]() 得
得![]() , 解得b=-6
, 解得b=-6
![]() 抛物线的解析式为
抛物线的解析式为![]() ,对称轴为直线x=3
,对称轴为直线x=3
令x=3得y=-9
![]() B(3,-9)
B(3,-9)
( 2 )由题意四边形ODGF为平行四边形
![]() FG=OD=2
FG=OD=2
![]() FG||轴
FG||轴
![]()
![]() G在抛物线.上
G在抛物线.上
![]() 在
在![]() 中令x=5得y=-5 ,
中令x=5得y=-5 ,![]() G(5,-5)
G(5,-5)
可求得直线DG解析式为: ![]()
![]() E在对称轴直线x=3与DG交点
E在对称轴直线x=3与DG交点
![]() 在
在![]() 中令x=3得y=
中令x=3得y=![]()
![]()
(3)可得E(3,-1) ,所以直线DG解析式为: y=-x+2
令x=5得y=-3 ,![]() G(5.-3)
G(5.-3)
所以直线BA解析式为: y=3x-18
在y=3x-18中令x=6得y=0 ,![]() A(6,0)在直线BG .上
A(6,0)在直线BG .上
( 4)四边形PFHG是平行四边形,理由如下:
在(3)的条件下G(5,-3) , CD=CE,∠CDE=45°
![]() DG\\OF
DG\\OF
![]() ∠FDC=∠CDE=45° ,可得CF=CO=3 ,
∠FDC=∠CDE=45° ,可得CF=CO=3 ,![]() F(3,-3)
F(3,-3)
可求得直线OF解析式为: y=-x ,与直线BA: y=3x-18联立可得![]()
由两点距离公式可求得DG=![]() ,由于P为DG中点,所以PG=
,由于P为DG中点,所以PG=![]() FH=
FH=![]()
![]() PG= FH
PG= FH
又![]() PG\\FH
PG\\FH
![]() 四边形PFHG是平行四边形
四边形PFHG是平行四边形
问题情境:
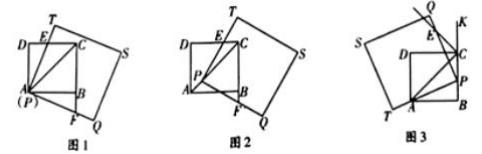
已知AC是正方形ABCD的对角线,将正方形PQST和正方形ABCD按如图放置.
(1)如图1,使点P与点A重合,PT与DC相交与点E, PQ与CB的延长线相交于点F.求证: AF=AE
(2)如图2,使点P在AC上(A, C两点除外),PT与DC相交与点E, PQ与CB的延长线相交与点F.判断PE和PF的数量关系,并说明理由.
拓广探索:
(3) 如图3,使P在BC上(B,C两点除外), PT经过点A, PQ与正方形ABCD的外角∠DCK的平分线CE相交与点E.判断PA和PE的数量关系,并说明理由.
考点:正方形与全等三角形综合
答案:见解析
解析:( 1 )手拉手全等可以证明![]() MDE≌
MDE≌![]() ABF(AS)
ABF(AS)
![]() AF=AE
AF=AE
(2)PE=PF ,理由如下:
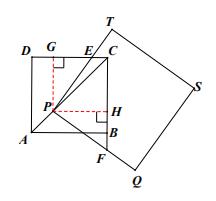
过点P作PG⊥DC于点G,作PH⊥BC于点H
![]() 四边形PQST是正方形
四边形PQST是正方形
![]() ∠QPT= 90°
∠QPT= 90°
![]() 四边形ABCD是正方形
四边形ABCD是正方形
![]() CP平分∠DCB,∠BCD= 90°
CP平分∠DCB,∠BCD= 90°
又![]() PG⊥DC于点G,PH⊥BC于点H
PG⊥DC于点G,PH⊥BC于点H
![]() PG= PH
PG= PH
![]() PG⊥DC,PH⊥BC
PG⊥DC,PH⊥BC
![]() ∠PGC=90°,∠PHC= 90°
∠PGC=90°,∠PHC= 90°
在四边形PHCG中,∠PGC=90°,∠PHC=90°,∠GCH = 90°
![]() ∠GPH= 360°-∠PGC-∠GCH- ∠PHC= 360°- 90°- 90°- 90°= 90°
∠GPH= 360°-∠PGC-∠GCH- ∠PHC= 360°- 90°- 90°- 90°= 90°
![]() ∠GPE+∠EPH =90°
∠GPE+∠EPH =90°
![]() ∠QPT= 90°
∠QPT= 90°
![]() ∠EPH+∠HPF = 90°
∠EPH+∠HPF = 90°
![]() ∠GPE=∠HPF
∠GPE=∠HPF
![]()
![]() PGE≌
PGE≌![]() PHF( ASA)
PHF( ASA)
![]() PE= PF
PE= PF
(3)PA=PE ,理由如下:
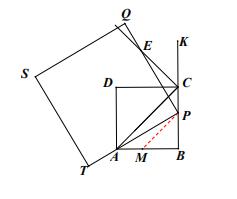
在BA上取点M使得BM=BP,连接PM
![]() 四边形PQST是正方形
四边形PQST是正方形
![]() ∠QPT= 90°
∠QPT= 90°
![]() ∠CPE+∠BPA= 90° .
∠CPE+∠BPA= 90° .
![]() 四边形ABCD是正方形
四边形ABCD是正方形
![]() AB=BC,∠B=90°,∠ BCD= 90°
AB=BC,∠B=90°,∠ BCD= 90°
在![]() ABP中∠B=90°,
ABP中∠B=90°,![]() ∠BAP+∠BPA=90°
∠BAP+∠BPA=90°
![]() ∠CPE=∠B4P
∠CPE=∠B4P
![]() AB=BC,BM=BP
AB=BC,BM=BP
AB-BM= BC- BP即AM= PC .
![]() ∠B=90°,BM=BP
∠B=90°,BM=BP
![]()
![]() BMP是等腰直角三E角形,
BMP是等腰直角三E角形,![]() ∠BMP= 45°
∠BMP= 45°
![]() ∠AMP=180°-∠BMP= 180°- 45°= 135°
∠AMP=180°-∠BMP= 180°- 45°= 135°
![]() CE平分∠DCK
CE平分∠DCK
![]() ∠DCE=
∠DCE=![]() ∠DCK=45° .
∠DCK=45° .
![]() ∠PCE=∠PCD+∠DCE=90° +45°= 135°
∠PCE=∠PCD+∠DCE=90° +45°= 135°
![]() ∠AMP=∠PCE
∠AMP=∠PCE
![]() ∠CPE=∠BAP,AM=PC,∠AMP=∠PCE
∠CPE=∠BAP,AM=PC,∠AMP=∠PCE
![]()
![]() AMP≌
AMP≌![]() PCE(ASA)
PCE(ASA)
![]() PA=PE
PA=PE
2020年新冠肺炎疫情发生以来,每天测体温成为一种制度,手持红外测温枪成为紧俏商品.某经销店承诺对所有商品明码标价,绝不哄抬物价.如下表所示是该店甲、乙两种手持红外测温枪的进价和售价:该店有一批用38000元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共4000元(毛利润= (售价-进价) x销售量)
(1)该店库存的甲、乙两种手持红外测温枪分别为多少个?
(2)根据销售情况,该店计划增加甲种手持红外测温枪的购进量,减少乙种手持红外测温枪的购进量已知甲种手持红外测温枪增加的数量是乙种手持红外测温枪减少的数量的3倍,进货价不变,而且用于购进这两种手持红外测温枪的总资金不超过40000元,则该店怎样进货,可使全部销售后获得的毛利润最大?并求出最大毛利润

考点:方程组与不等式的应用
答案:见解析
解析: (1)设该店库存手持红外线测温枪中甲种有x个,乙种有y个
由题意,得![]()
解得![]()
答:甲种20个,乙种30个.
(2)设乙种手持红外测温枪减少a个,则甲种增加3a个
400(20+ 3a)+ 1000(30-a)≤4000
解得a≤10
设全部销售后的毛利润为W
W=(450- 400)(20+ 3a)+(1100- 1000)(30-a)= 50a +400
![]() 50>0
50>0
![]() W随a的增大而增大
W随a的增大而增大
![]() 当a=10时,
当a=10时,![]() =4500 .
=4500 .
答:购进甲种50个,乙种20个可使毛利润最大,最大毛利润为4500元
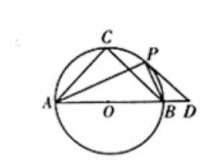
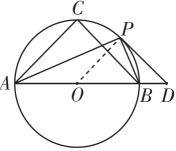
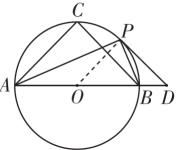
如图,已知![]() ABC内接于圆O,AB为圆O的直径,且AC= BC=
ABC内接于圆O,AB为圆O的直径,且AC= BC=![]() ,点P为BC.上任意一点(不与B, C重合),PD与圆O相切于点P,交AB的延长线于点D,连接PA,PB.
,点P为BC.上任意一点(不与B, C重合),PD与圆O相切于点P,交AB的延长线于点D,连接PA,PB.
(1)若PD//BC,求证:∠CAP=∠PAB
(2)若PB=BD,求PD的长度.
考点:圆中证明与计算
答案:见解析
解析:(1)证明:连接OP, ![]() PD是切线
PD是切线
![]() ∠OPD=90° ,又
∠OPD=90° ,又![]() ∠APB=90°
∠APB=90°
![]() ∠APB-∠OPB=∠OPD-∠OPB ,即∠OPA=∠BPD
∠APB-∠OPB=∠OPD-∠OPB ,即∠OPA=∠BPD
![]() 0A= OP
0A= OP
![]() ∠PAB=∠OPA=∠BPD①
∠PAB=∠OPA=∠BPD①
![]() PD//BC
PD//BC
![]() ∠BPD=∠PBC
∠BPD=∠PBC
又![]() ∠PBC=∠CAP ( 圆周角相等)
∠PBC=∠CAP ( 圆周角相等)
![]() ∠CAP=∠BPD②
∠CAP=∠BPD②
![]() ∠CAP=∠PAB
∠CAP=∠PAB
(2)连接OP,则![]() OPD为直角三角形
OPD为直角三角形
![]() PB= BD
PB= BD
![]() ∠BPD=∠D
∠BPD=∠D
又![]() ∠BPD+∠BPO=90°,∠D+∠BOP= 90°
∠BPD+∠BPO=90°,∠D+∠BOP= 90°
![]() ∠BOP=∠BPO
∠BOP=∠BPO
![]() BP=BO(BP为斜边中线)
BP=BO(BP为斜边中线)
在Rt![]() ACB中,AB=
ACB中,AB=![]() AC=12,OB=
AC=12,OB=![]() AB=6
AB=6
![]() OD=OB+ BD= 20B=12,OP= 6
OD=OB+ BD= 20B=12,OP= 6
在Rt![]() OPD中,
OPD中,![]()
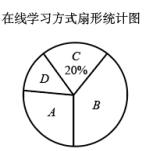
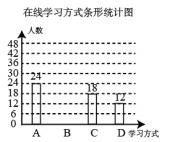
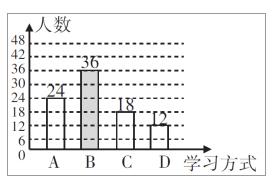
学校为了解疫情期间学生自习课落“停课不停学、学习不延期"在线学习的效果,王校长通过网络学习平台,随机抽查了该校部分学生在一节自习课中的学习情况,发现共有四种学习方式(每人只参与其中一种): A.阅读电子教材,B.听教师录播课程,C.完成在线作业,D线上讨论交流.并根据调查结果绘制成如下两幅不完整的统计图,根据图中信息,解答下列问题:
(1)直接写出王校长本次调查的学生总人数是_____, 并补全条形统计图:
(2)求扇形统计图中“D.线上讨论交流”对应的圆心角的度数;
(3)该校在线学习学生共有4000人,请你估计“B.听教师录播课程"有多少人:
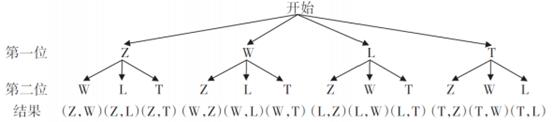
(4)王校长想从4位辅导教师(分别记为Z, W, L, T)中,随机选择两位进行电话访谈.请用列表或画树状图的方法求出选中Z老师的概率.
考点:概率与统计
答案:见解析
解析: (1) 90,如图所示:

本卷还有18题,登录并加入会员即可免费使用哦~

该作品由: 用户小小分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。