人教版初中数学单元测试136140
初中
整体难度：中等
2020-01-10
题号
一
二
三
四
五
评分
一、解答题 (共8题)
添加该题型下试题
1.
细心观察图形，认真分析各式，然后解答问题：
OA1＝1；
OA2＝
＝
； S1＝
×1×1＝；
OA3＝
＝
； S2＝××1＝
；
OA4＝
＝
； S3＝
×
×1＝
；
（1）推算出OA10＝ ．
（2）若一个三角形的面积是
．则它是第 个三角形．
（3）用含n（n是正整数）的等式表示上述面积变化规律；
（4）求出S12+S22+S23+…+S2100的值．
难度：
知识点：二次根式
使用次数：54
【答案】
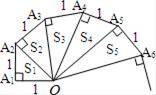
解：（1））∵OAn2＝n，
∴OA10＝
．
故答案为：；
（2）若一个三角形的面积是
，
∵Sn＝
＝
，
∴
＝2＝
，
∴它是第20个三角形．
故答案为：20；
（3）结合已知数据，可得：OAn2＝n；Sn＝
；
（4）S12+S22+S23+…+S2100
＝
+
+
+
+…+
＝
＝
2.
观察下列各式：
＝1+
﹣
＝1；
＝1+﹣
＝1
；
＝1+
﹣
＝1
，…
请你根据以上三个等式提供的信息解答下列问题
①猜想：
＝ ＝ ；
②归纳：根据你的观察，猜想，请写出一个用n（n为正整数）表示的等式： ；
③应用：计算
．
难度：
知识点：二次根式的乘除
使用次数：157
【答案】
．解：①猜想：
＝1+
﹣
＝1
；
故答案为：1+﹣，1；
②归纳：根据你的观察，猜想，写出一个用n（n为正整数）表示的等式：
＝1+
﹣
＝
；
③应用：
＝
＝
＝1+
﹣
＝1
．
3.
阅读材料：
小明在学习二次根式的化简后，遇到了这样一个需要化简的式子：
．该如何化简呢？思考后，他发现3+2
＝1+2+（）2＝（1+）2．于是
＝
＝1+
．善于思考的小明继续深入探索；当a+b＝（m+n）2时（其中a，b，m，n均为正整数），则a+b＝m2+2mn+2n2．此时，a＝m2+2n2，b＝2mn，于是，
＝m+n．请你仿照小明的方法探索并解决下列何题：
（1）设a，b，m，n均为正整数且
＝m+n
，用含m，n的式子分别表示a，b时，结果是a＝ ，b＝ ；
（2）利用（1）中的结论，选择一组正整数填空：
＝ + ；
（3）化简：
．
难度：
知识点：二次根式的乘除
使用次数：190
【答案】
解：（1）由题意得：a+b
＝（m+n）2，
∴a+b＝m2+3n2+2mn，
∴a＝m2+3n2，b＝2mn；
故答案为：m2+3n2；2mn；
（2）取m＝2，n＝1，则a＝m2+3n2＝7，b＝2mn＝4，
7+4＝（2+）2；
故答案为：
，2，1；
（3）
＝
＝
+1．
4.
如图：面积为48cm2的正方形四个角是面积为3cm2的小正方形，现将四个角剪掉，制作一个无盖的长方体盒子，求这个长方体盒子的底面边长和体积分别是多少？（精确到0.1cm，≈1.732）
难度：
知识点：二次根式的乘除
使用次数：115
【答案】
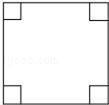
解：正方形的边长＝
＝4
cm，
剪掉小正方形的边长＝cm，
所以，长方体盒子的底面边长＝4﹣2＝2≈2×1.732≈3.5cm，
体积＝（2）2•＝12≈12×1.732≈20.8cm3．
答：这个长方体盒子的底面边长是3.5cm，体积是20.8cm3．
5.
已知a＝
，b＝
，
（1）求ab，a+b的值；
（2）求
的值．
难度：
知识点：二次根式的加减
使用次数：124
【答案】
解：（1）∵a＝
＝
＝
+
，b＝＝
＝﹣，
∴ab＝（+）×（﹣
）＝1，
a+b＝
++﹣＝2；
（2）
＝
+
＝（﹣）2+（+）2
＝5﹣2
+5+2
＝10．
本卷还有19题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
24
总体难度：
中等
难度统计
难度系数
数量
占比
中等
12
50.0%
容易
12
50.0%
题型统计
大题类型
数量
占比
解答题
8
33.33%
计算题
2
8.33%
填空题
4
16.66%
选择题
10
41.66%
知识点统计
知识点
数量
占比
二次根式
7
29.16%
二次根式的乘除
9
37.5%
二次根式的加减
8
33.33%
版权提示
该作品由: 用户千顺分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。