如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,与y轴相交于点C,直线y=kx+n(k≠0)经过B,C两点,已知A(1,0),C(0,3),且BC=5.
(1)分别求直线BC和抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得以B,C,P三点为顶点的三角形是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
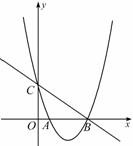
【解答】(1)∵C(0,3),即OC=3,BC=5,∴在Rt△BOC中,根据勾股定理得:OB=![]() =4,即B(4,0),把B与C坐标代入y=kx+n中,得:
=4,即B(4,0),把B与C坐标代入y=kx+n中,得: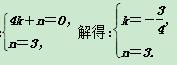 ∴直线BC解析式为y=-
∴直线BC解析式为y=-![]() x+3.由A(1,0),B(4,0),设抛物线解析式为y=a(x-1)(x-4),把C(0,3)代入得:a=
x+3.由A(1,0),B(4,0),设抛物线解析式为y=a(x-1)(x-4),把C(0,3)代入得:a=![]() ,则抛物线解析式为y=
,则抛物线解析式为y=![]() x2-
x2-![]() x+3.
x+3.
(2)存在.如图所示,分两种情况考虑:∵抛物线解析式为y=![]() x2-
x2-![]() x+3,∴其对称轴为直线x=
x+3,∴其对称轴为直线x=![]() .设点P坐标为(
.设点P坐标为(![]() ,y),BC与对称轴交于点Q,可得Q点坐标(
,y),BC与对称轴交于点Q,可得Q点坐标(![]() ,
,![]() ),同时可求得CQ=
),同时可求得CQ=![]() ,BQ=
,BQ=![]() .当P1C⊥CB时,△P1BC为直角三角形.P1C2=(
.当P1C⊥CB时,△P1BC为直角三角形.P1C2=(![]() )2+(y-3)2,P1Q=y-
)2+(y-3)2,P1Q=y-![]() .∵P1Q2=P1C2+CQ2.解得y=
.∵P1Q2=P1C2+CQ2.解得y=![]() ;当P2B⊥BC时,△BCP2为直角三角形.P2B2=(4-
;当P2B⊥BC时,△BCP2为直角三角形.P2B2=(4-![]() )2+y2,P2Q=
)2+y2,P2Q=![]() -y,∵P2Q2=P2B2+BQ2,解得y=-2.综上所述,P1(
-y,∵P2Q2=P2B2+BQ2,解得y=-2.综上所述,P1(![]() ,
,![]() )或P2(
)或P2(![]() ,-2).当点P为直角顶点时,设P(
,-2).当点P为直角顶点时,设P(![]() ,y),∵B(4,0),C(0,3),∴BC=5,∴BC2=PC2+PB2,即25=(
,y),∵B(4,0),C(0,3),∴BC=5,∴BC2=PC2+PB2,即25=(![]() )2+(y-3)2+(
)2+(y-3)2+(![]() -4)2+y2,解得y=
-4)2+y2,解得y=![]() ,∴P3(
,∴P3(![]() ,
,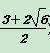 ),P4(
),P4(![]() ,
,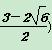 ).综上所述,P1(
).综上所述,P1(![]() ,
,![]() ),P2(
),P2(![]() ,-2),P3(
,-2),P3(![]() ,
,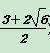 ),P4(
),P4(![]() ,
,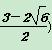 ).
).
某服装店购进一批秋衣,价格为每件30元.物价部门规定其销售单价不高于每件60元,经市场调查发现:日销售量y(件)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围;
(2)求该服装店销售这批秋衣日获利W(元)与销售单价x(元)之间的函数关系式;
(3)当销售单价为多少元时,该服装店日获利最大?最大获利是多少元?
解析】:(1)设y=kx+b,根据题意得![]() 解得k=-2,b=200,故y=-2x+200(30≤x≤60).
解得k=-2,b=200,故y=-2x+200(30≤x≤60).
(2)W=(x-30)(-2x+200)-450=-2x2+260x-6450=-2(x-65)2+2000.(3)W=-2(x-65)2+2000,∵a=-2<0,30≤x≤60,∴在x取值范围内,W随x的增大而增大,则当x=60时,W有最大值为1950元,∴当销售单价为60元时,该服装店日获利最大,为1950元.
如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.
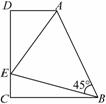
解析】过点B作DA的垂线交DA的延长线于点M,M为垂足,延长DM到G,使MG=CE,连接BG,易知四边形BCDM是正方形,在△BEC与△BGM中,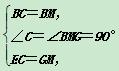 ∴△BEC≌△BGM(SAS),∴∠MBG=∠CBE,BE=BG.∵∠ABE=45°,∴∠CBE+∠ABM=∠MBG+∠ABM=45°,即∠ABE=∠ABG=45°.在△ABE与△ABG中,
∴△BEC≌△BGM(SAS),∴∠MBG=∠CBE,BE=BG.∵∠ABE=45°,∴∠CBE+∠ABM=∠MBG+∠ABM=45°,即∠ABE=∠ABG=45°.在△ABE与△ABG中,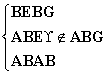 ,∴△ABE≌△ABG(SAS),∴AG=AE=10.设CE=x,则AM=10-x,AD=12-(10-x)=2+x,DE=12-x.在Rt△ADE中,AE2=AD2+DE2,∴100=(x+2)2+(12-x)2,即x2-10x+24=0,解得:x1=4,x2=6.故CE的长为4或6.
,∴△ABE≌△ABG(SAS),∴AG=AE=10.设CE=x,则AM=10-x,AD=12-(10-x)=2+x,DE=12-x.在Rt△ADE中,AE2=AD2+DE2,∴100=(x+2)2+(12-x)2,即x2-10x+24=0,解得:x1=4,x2=6.故CE的长为4或6.
某地2015年为做好“精准扶贫”,投入资金1 280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1 600万元.
(1)从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?
(2)在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1 000户(含第1 000户)每户每天奖励8元,1 000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?
解析】(1)设该地投入异地安置资金的年平均增长率为x,根据题意,得1280(1+x)2=1 280+1 600,解得x=0.5或x=-2.5(舍),答:从2015年到2017年,该地投入异地安置资金的年平均增长率为50%.
(2)设今年该地有a户享受到优先搬迁租房奖励,根据题意,得:1 000×8×400+(a-1 000)×5×400≥5 000 000,解得:a≥1 900,答:今年该地至少有1 900户享受到优先搬迁租房奖励.
如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于点B,OC=BC,AC=![]() OB.
OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦AD的长.
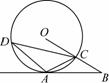
【解析】(1)如图,连接OA.∵AC=![]() OB,OC=CB,∴AC=OC=CB,∴∠OAB=90°,∴AB是⊙O的切线.
OB,OC=CB,∴AC=OC=CB,∴∠OAB=90°,∴AB是⊙O的切线.
(2)如图,连接OD.∵∠DOA=2∠DCA,∠DCA=45°,∴∠DOA=90°.∵OD=OA=OC=2,∴AD=![]() =2
=2![]() .
.
本卷还有19题,登录并加入会员即可免费使用哦~

该作品由: 用户王振分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。