2019四川九年级上学期人教版初中数学期中考试132857
初中
整体难度：中等
2018-11-01
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
用因式分解法解一元二次方程x（x﹣3）=x﹣3时，原方程可化为（ ）
A．（x﹣1）（x﹣3）=0 B．（x+1）（x﹣3）=0 C．x （x﹣3）=0 D．（x﹣2）（x﹣3）=0
难度：
知识点：解一元二次方程
使用次数：147
【答案】
A 解：x（x﹣3）=x﹣3，
x（x﹣3）﹣（x﹣3）=0，
（x﹣3（x﹣1）=0，
故选A．
【点评】本题考查了解一元二次方程的应用，能正确分解因式是解此题的关键．
2.
随机掷一枚均匀的硬币两次，两次正面都朝上的概率是（ ）
A．
B．
C．
D．1
难度：
知识点：随机事件与概率
使用次数：129
【答案】
A解：随机掷一枚均匀的硬币两次，
可能的结果有：正正，正反，反正，反反，
∴两次正面都朝上的概率是．
3.
下列各组线段中是成比例线段的是（ ）
A．1cm，2cm，3cm，4cm B．1cm，2cm，2cm，4cm
C．3cm，5cm，9cm，13cm D．1cm，2cm，2cm，3cm
难度：
知识点：图形的相似
使用次数：171
【答案】
B解：∵1×4≠2×3，
∴选项A不成比例；
∵1×4=2×2，
∴选项B成比例；
∵3×13≠5×9，
∴选项C不成比例；
∵3×1≠2×2，
∴选项D不成比例
4.
关于x的方程x2+（m﹣2）x+m+1=0有两个相等的实数根，则m的值是（ ）
A．0 B．8 C．4
D．0或8
难度：
知识点：解一元二次方程
使用次数：170
【答案】
D解：∵方程x2+（m﹣2）x+m+1=0有两个相等的实数根，
∴△=0，即（m﹣2）2﹣4（m+1）=0，
解得：m=0或m=8，
5.
如图，三角形ABC中，D、E、F分别是AB，AC，BC上的点，且DE∥BC，EF∥AB，AD：DB=1：2，BC=30cm，则FC的长为（ ）
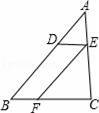
A．10cm B．20cm C．5cm D．6cm
难度：
知识点：平行四边形
使用次数：157
【答案】
B解：∵DE∥BC，EF∥AB，
∴四边形BDEF是平行四边形，
∴BF=DE．
∵AD：DB=1：2，
∴AD：AB=1：3．
∵DE∥BC，
∴DE：BC=AD：AB=1：3，即DE：30=1：3，
∴DE=10，
∴BF=10．
故FC的长为20cm．
本卷还有20题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
25
总体难度：
中等
难度统计
难度系数
数量
占比
容易
17
68.0%
中等
8
32.0%
题型统计
大题类型
数量
占比
选择题
10
40.0%
填空题
6
24.0%
计算题
2
8.0%
解答题
7
28.00%
知识点统计
知识点
数量
占比
解一元二次方程
8
32.0%
随机事件与概率
1
4.0%
图形的相似
2
8.0%
平行四边形
2
8.0%
相似三角形
2
8.0%
实际问题与一元二次方程
3
12.0%
特殊的平行四边形
4
16.0%
三角形全等的判定
1
4.0%
用列举法求概率
1
4.0%
勾股定理
1
4.0%
版权提示
该作品由: 用户彭分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。