2018广东九年级上学期北师大版初中数学单元测试132479
初中
整体难度：中等
2018-09-21
题号
一
二
三
四
五
评分
一、解答题 (共9题)
添加该题型下试题
1.
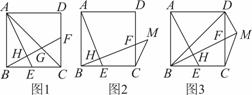
已知正方形ABCD中，点E，F分别为BC，CD上的点，连接AE，BF相交于点H，且AE⊥BF.
(1)如图1，连接AC交BF于点G，求证：∠AGF＝∠AEB＋45°；
(2)如图2，延长BF到点M，连接MC，若∠BMC＝45°，求证：AH＋BH＝BM；
(3)如图3，在(2)的条件下，若点H为BM的三等分点，连接BD，DM，若HE＝1，求△BDM的面积．
难度：
知识点：特殊的平行四边形
使用次数：102
【答案】
解：
(1)∵四边形ABCD是正方形，∴∠ABC＝∠BCD＝90°，∴∠ACB＝∠ACD＝45°，∵AE⊥BF，∴∠AEB＋∠FBC＝90°，∵∠FBC＋∠BFC＝90°∴∠AEB＝∠BFC，∵∠AGF＝∠BFC＋∠ACF，∴∠AGF＝∠AEB＋45° (2)过C作CK⊥BM于K，∴∠BKC＝∠AHB＝90°，∵∠BMC＝45°，∴CK＝MK，∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝∠BCD＝90°，∴∠ABH＝∠BCK，∴△ABH≌△BCK(AAS)，∴BH＝CK＝MK，AH＝BK，∴BM＝BK＋MK＝AH＋BH (3)由(2)得，BH＝CK＝MK，∵H为BM的三等分点，∴BH＝HK＝KM，过E作EN⊥CK于N，∴四边形HENK是矩形，∴HK＝EN＝BH，∠BHE＝∠ENC，∴△BHE≌△ENC(ASA)，∴HE＝CN＝NK＝1，∴CK＝BH＝2，∴BM＝6，连接CH，∵HK＝MK，CK⊥MH，∠BMC＝45°，∴CH＝CM，∠MCH＝90°，∴∠BCH＝∠DCM，∴△BHC≌△DMC(SAS)，∴BH＝DM＝2，∠BHC＝∠DMC＝135°，∴∠DMB＝90°，∴△BDM的面积为
DM·BM＝6
2.
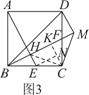
如图，在Rt△ABC中，∠B＝90°，AC＝60 cm，∠A＝60°，点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是t s(0＜t≤15)．过点D作DF⊥BC于点F，连接DE，EF.
(1)求证：AE＝DF；
(2)四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；
(3)当t为何值时，△DEF为直角三角形？请说明理由．
难度：
知识点：特殊的平行四边形
使用次数：59
【答案】
解：(1)∵∠DFC＝90°，∠C＝30°，DC＝4t，∴DF＝2t，又∵AE＝2t，∴AE＝DF (2)能，理由：∵AB⊥BC，DF⊥BC，∴AE∥DF，又∵AE＝DF，∴四边形AEFD为平行四边形，当AE＝AD时，四边形AEFD为菱形，即60－4t＝2t，解得t＝10，∴当t＝10秒时，四边形AEFD为菱形 (3)①当∠DEF＝90°时，由(1)知四边形AEFD为平行四边形，∴EF∥AD，∴∠ADE＝∠DEF＝90°，∵∠A＝60°，∴∠AED＝30°，∴AD＝AE＝t，又AD＝60－4t，即60－4t＝t，解得t＝12；②当∠EDF＝90°时，四边形EBFD为矩形，在Rt△AED中∠A＝60°，则∠ADE＝30°，∴AD＝2AE，即60－4t＝4t，解得t＝
；③若∠EFD＝90°，则E与B重合，D与A重合，此种情况不存在．综上所述，当t＝ s或12 s时，△DEF为直角三角形
3.
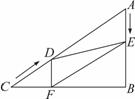
如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点C′处，折痕为EF.
(1)求证：BE＝BF；
(2)若∠ABE＝20°，求∠BFE的度数；
(3)若AB＝6，AD＝8，求AE的长．
难度：
知识点：特殊的平行四边形
使用次数：86
【答案】
解：(1)由题意得∠BEF＝∠DEF.∵四边形ABCD为矩形，∴DE∥BF，∴∠BFE＝∠DEF，∴∠BEF＝∠BFE，∴BE＝BF (2)∵四边形ABCD为矩形，∴∠ABF＝90°；而∠ABE＝20°，∴∠EBF＝90°－20°＝70°；又∵∠BEF＝∠BFE，∴∠BFE的度数为55° (3)由题意知BE＝DE；设AE＝x，则BE＝DE＝8－x，由勾股定理得(8－x)2＝62＋x2，解得x＝
，即AE的长为
4.
如图，在△ABC中，∠ACB＝90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE的延长线上，且AF＝CE＝AE.
(1)求证：四边形ACEF是平行四边形；
(2)当∠B满足什么条件时，四边形ACEF是菱形，并说明理由．
难度：
知识点：特殊的平行四边形
使用次数：67
【答案】
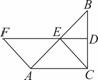
解：(1)由题意知∠FDC＝∠DCA＝90°，∴EF∥CA，∴∠AEF＝∠EAC.∵AF＝CE＝AE，∴∠F＝∠AEF＝∠EAC＝∠ECA.又∵AE＝EA，∴△AEC≌△EAF，∴EF＝CA，∴四边形ACEF是平行四边形 (2)当∠B＝30°时，四边形ACEF是菱形．理由：∠B＝30°，∠ACB＝90°，∴AC＝AB.∵DE垂直平分BC，∴BE＝CE.∵AE＝CE，∴AE＝BE＝CE＝AB，∴AC＝CE，由(1)得四边形ACEF是平行四边形，∴四边形ACEF是菱形
5.
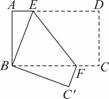
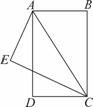
如图，已知BA＝AE＝DC，AD＝EC，CE⊥AE，垂足为E.
(1)求证：△DCA≌△EAC；
(2)只需添加一个条件，即AD＝BC(答案不唯一)，可使四边形ABCD为矩形，请加以证明．
难度：
知识点：特殊的平行四边形
使用次数：101
【答案】
解：(1)在△DCA和△EAC中，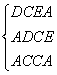
∴△DCA≌△EAC(SSS) (2)添加AD＝BC，可使四边形ABCD为矩形．理由：∵AB＝DC，AD＝BC，∴四边形ABCD是平行四边形．∵CE⊥AE，∴∠E＝90°，由(1)知△DCA≌△EAC，∴∠D＝∠E＝90°，∴四边形ABCD为矩形
本卷还有20题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
25
总体难度：
中等
难度统计
难度系数
数量
占比
中等
10
40.0%
容易
15
60.0%
题型统计
大题类型
数量
占比
解答题
9
36.0%
填空题
6
24.0%
选择题
10
40.0%
知识点统计
知识点
数量
占比
特殊的平行四边形
24
96.0%
平行四边形
1
4.0%
版权提示
该作品由: 用户111111111分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。