2018湖北人教版初中数学中考真题132260
初中
整体难度：中等
2018-08-24
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
下列代数式中，整式为（ ）
A．x+1 B．
C．
D．
难度：
知识点：各地中考
使用次数：176
【答案】
A【分析】直接利用整式、分式、二次根式的定义分析得出答案．
【解答】解：A、x+1是整式，故此选项正确；
B、
，是分式，故此选项错误；
C、是二次根式，故此选项错误；
D、，是分式，故此选项错误；
故选：A．
2.
如图，两个实数互为相反数，在数轴上的对应点分别是点A、点B，则下列说法正确的是（ ）
A．原点在点A的左边 B．原点在线段AB的中点处
C．原点在点B的右边 D．原点可以在点A或点B上
难度：
知识点：各地中考
使用次数：105
【答案】
B分析】根据互为相反数的两个数，它们分别在原点两旁且到原点距离相等解答．
【解答】解：∵点A、点B表示的两个实数互为相反数，
∴原点在到在线段AB上，且到点A、点B的距离相等，
∴原点在线段AB的中点处，
故选：B．
【点评】本题考查的是实数与数轴、相反数的概念，掌握互为相反数的两个数，它们分别在原点两旁且到原点距离相等是解题的关键．
3.
下列计算正确的是（ ）
A．3a2﹣4a2=a2 B．a2•a3=a6 C．a10÷a5=a2 D．（a2）3=a6
【分析】根据合并同类项法则，单项式的乘法运算法则，单项式的除法运算法则，对各选项
难度：
知识点：各地中考
使用次数：183
【答案】
D【解答】解：A、3a2﹣4a2=﹣a2，错误；
B、a2•a3=a5，错误；
C、a10÷a5=a5，错误；
D、（a2）3=a6，正确；
故选：D．
【点评】本题考查了整式的除法，单项式的乘法，合并同类项法则，是基础题，熟记运算法则是解题的关键．
4.
如图，两条直线l1∥l2，Rt△ACB中，∠C=90°，AC=BC，顶点A、B分别在l1和l2上，∠1=20°，则∠2的度数是（ ）
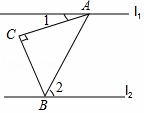
A．45° B．55° C．65° D．75°
难度：
知识点：各地中考
使用次数：111
【答案】
C【分析】根据平行线的性质和等腰直角三角形的性质解答即可．
【解答】解：∵l1∥l2，
∴∠1+∠CAB=∠2，
∵Rt△ACB中，∠C=90°，AC=BC，
∴∠CAB=45°，
∴∠2=20°+45°=65°，
故选：C．
5.
解分式方程
﹣3=
时，去分母可得（ ）
A．1﹣3（x﹣2）=4 B．1﹣3（x﹣2）=﹣4 C．﹣1﹣3（2﹣x）=﹣4 D．1﹣3（2﹣x）=4
难度：
知识点：各地中考
使用次数：107
【答案】
B解：去分母得：1﹣3（x﹣2）=﹣4，
故选：B．
【点评】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．
本卷还有21题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
26
总体难度：
中等
难度统计
难度系数
数量
占比
中等
10
38.46%
容易
15
57.69%
偏难
1
3.84%
题型统计
大题类型
数量
占比
选择题
10
38.46%
填空题
8
30.76%
计算题
2
7.69%
解答题
5
19.23%
综合题
1
3.84%
知识点统计
知识点
数量
占比
各地中考
26
100.0%
版权提示
该作品由: 用户魏伟分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。