2018江苏苏科版初中数学中考真题131879
初中
整体难度：中等
2018-07-09
题号
一
二
三
四
五
评分
一、解答题 (共7题)
添加该题型下试题
1.
平面直角坐标系xOy中，横坐标为a的点A在反比例函数y1═
（x＞0）的图象上，点A′与点A关于点O对称，一次函数y2=mx+n的图象经过点A′．
（1）设a=2，点B（4，2）在函数y1、y2的图象上．
①分别求函数y1、y2的表达式；
②直接写出使y1＞y2＞0成立的x的范围；
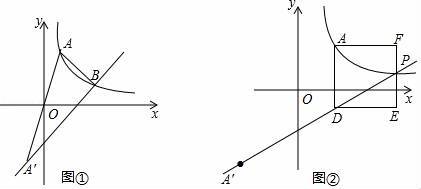
（2）如图①，设函数y1、y2的图象相交于点B，点B的横坐标为3a，△AA'B的面积为16，求k的值；
（3）设m=
，如图②，过点A作AD⊥x轴，与函数y2的图象相交于点D，以AD为一边向右侧作正方形ADEF，试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上．
难度：
知识点：各地中考
使用次数：156
【答案】
【分析】（1）由已知代入点坐标即可；
（2）面积问题可以转化为△AOB面积，用a、k表示面积问题可解；
（3）设出点A、A′坐标，依次表示AD、AF及点P坐标．
【解答】解：（1）①由已知，点B（4，2）在y1═
（x＞0）的图象上
∴k=8
∴y1=
∵a=2
∴点A坐标为（2，4），A′坐标为（﹣2，﹣4）
把B（4，2），A（﹣2，﹣4）代入y2=mx+n
解得
∴y2=x﹣2
②当y1＞y2＞0时，y1=
图象在y2=x﹣2图象上方，且两函数图象在x轴上方
∴由图象得：2＜x＜4
（2）分别过点A、B作AC⊥x轴于点C，BD⊥x轴于点D，连BO
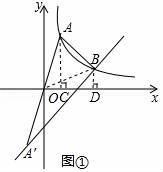
∵O为AA′中点
S△AOB=S△AOA′=8
∵点A、B在双曲线上
∴S△AOC=S△BOD
∴S△AOB=S四边形ACDB=8
由已知点A、B坐标都表示为（a，
）（3a，
）
∴
解得k=6
（3）由已知A（a，
），则A′为（﹣a，﹣）
把A′代入到y=
﹣
∴n=
∴A′B解析式为y=﹣
当x=a时，点D纵坐标为
∴AD=
∵AD=AF，
∴点F和点P横坐标为
∴点P纵坐标为
∴点P在y1═（x＞0）的图象上
【点评】本题综合考查反比例函数、一次函数图象及其性质，解答过程中，涉及到了面积转化方法、待定系数法和数形结合思想．
2.
平面直角坐标系xOy中，二次函数y=x2﹣2mx+m2+2m+2的图象与x轴有两个交点．
（1）当m=﹣2时，求二次函数的图象与x轴交点的坐标；
（2）过点P（0，m﹣1）作直线1⊥y轴，二次函数图象的顶点A在直线l与x轴之间（不包含点A在直线l上），求m的范围；
（3）在（2）的条件下，设二次函数图象的对称轴与直线l相交于点B，求△ABO的面积最大时m的值．
难度：
知识点：各地中考
使用次数：179
【答案】
【分析】（1）与x轴相交令y=0，解一元二次方程求解；
（2）应用配方法得到顶点A坐标，讨论点A与直线l以及x轴之间位置关系，确定m取值范围．
（3）在（2）的基础上表示△ABO的面积，根据二次函数性质求m．
【解答】解：（1）当m=﹣2时，抛物线解析式为：y=x2+4x+2
令y=0，则x2+4x+2=0
解得x1=﹣2+
，x2=﹣2﹣
抛物线与x轴交点坐标为：（﹣2+，0）（﹣2﹣，0）
（2）∵y=x2﹣2mx+m2+2m+2=（x﹣m）2+2m+2
∴抛物线顶点坐标为A（m，2m+2）
∵二次函数图象的顶点A在直线l与x轴之间（不包含点A在直线l上）
∴当直线1在x轴上方时
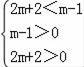
不等式无解
当直线1在x轴下方时
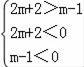
解得﹣3＜m＜﹣1
（3）由（1）
点A在点B上方，则AB=（2m+2）﹣（m﹣1）=m+3
△ABO的面积S=
（m+3）（﹣m）=﹣
∵﹣
∴当m=﹣
时，S最大=
【点评】本题以含有字母系数m的二次函数为背景，考查了二次函数图象性质以及分类讨论、数形结合的数学思想．
3.
日照间距系数反映了房屋日照情况．如图①，当前后房屋都朝向正南时，日照间距系数=L：（H﹣H1），其中L为楼间水平距离，H为南侧楼房高度，H1为北侧楼房底层窗台至地面高度．
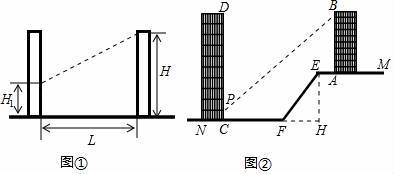
如图②，山坡EF朝北，EF长为15m，坡度为i=1：0.75，山坡顶部平地EM上有一高为22.5m的楼房AB，底部A到E点的距离为4m．
（1）求山坡EF的水平宽度FH；
（2）欲在AB楼正北侧山脚的平地FN上建一楼房CD，已知该楼底层窗台P处至地面C处的高度为0.9m，要使该楼的日照间距系数不低于1.25，底部C距F处至少多远？
难度：
知识点：各地中考
使用次数：156
【答案】
【分析】（1）在Rt△EFH中，根据坡度的定义得出tan∠EFH=i=1：0.75=
=
，设EH=4x，则FH=3x，由勾股定理求出EF=
=5x，那么5x=15，求出x=3，即可得到山坡EF的水平宽度FH为9m；
（2）根据该楼的日照间距系数不低于1.25，列出不等式
≥1.25，解不等式即可．
【解答】解：（1）在Rt△EFH中，∵∠H=90°，
∴tan∠EFH=i=1：0.75==
，
设EH=4x，则FH=3x，
∴EF=
=5x，
∵EF=15，
∴5x=15，x=3，
∴FH=3x=9．
即山坡EF的水平宽度FH为9m；
（2）∵L=CF+FH+EA=CF+9+4=CF+13，
H=AB+EH=22.5+12=34.5，H1=0.9，
∴日照间距系数=L：（H﹣H1）=
=
，
∵该楼的日照间距系数不低于1.25，
∴≥1.25，
∴CF≥29．
答：要使该楼的日照间距系数不低于1.25，底部C距F处29m远．
【点评】本题考查了解直角三角形的应用﹣坡度坡角问题，勾股定理，将实际问题转化为数学问题是解题的关键．
4.
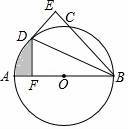
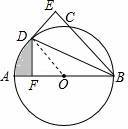
如图，AB为⊙O的直径，C为⊙O上一点，∠ABC的平分线交⊙O于点D，DE⊥BC于点E．
（1）试判断DE与⊙O的位置关系，并说明理由；
（2）过点D作DF⊥AB于点F，若BE=3
，DF=3，求图中阴影部分的面积．
难度：
知识点：各地中考
使用次数：154
【答案】
【分析】（1）直接利用角平分线的定义结合平行线的判定与性质得出∠DEB=∠EDO=90°，进而得出答案；
（2）利用勾股定理结合扇形面积求法分别分析得出答案．
【解答】解：（1）DE与⊙O相切，
理由：连接DO，
∵DO=BO，
∴∠ODB=∠OBD，
∵∠ABC的平分线交⊙O于点D，
∴∠EBD=∠DBO，
∴∠EBD=∠BDO，
∴DO∥BE，
∵DE⊥BC，
∴∠DEB=∠EDO=90°，
∴DE与⊙O相切；
（2）∵∠ABC的平分线交⊙O于点D，DE⊥BE，DF⊥AB，
∴DE=DF=3，
∵BE=3
，
∴BD=
=6，
∵sin∠DBF=
=，
∴∠DBA=30°，
∴∠DOF=60°，
∴sin60°=
=
=
，
∴DO=2
，
则FO=，
故图中阴影部分的面积为：
﹣××3=2π﹣
．
【点评】此题主要考查了切线的判定方法以及扇形面积求法等知识，正确得出DO的长是解题关键．
5.
）为了改善生态环境，某乡村计划植树4000棵．由于志题者的支援，实际工作效率提高了20%，结果比原计划提前3天完成，并且多植树80棵，原计划植树多少天？
难度：
知识点：各地中考
使用次数：136
【答案】
【解答】解：设原计划每天种x棵树，则实际每天种（1+20%）x棵，
依题意得：
﹣
=3
解得x=200，
经检验得出：x=200是原方程的解．
所以
=20．
答：原计划植树20天．
【点评】此题主要考查了分式方程的应用，正确理解题意，找出题目中的等量关系，列出方程是解题关键．
本卷还有22题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
27
总体难度：
中等
难度统计
难度系数
数量
占比
中等
14
51.85%
容易
12
44.44%
基础
1
3.70%
题型统计
大题类型
数量
占比
解答题
7
25.92%
综合题
1
3.70%
选择题
7
25.92%
计算题
3
11.11%
填空题
9
33.33%
知识点统计
知识点
数量
占比
各地中考
27
100.0%
版权提示
该作品由: 用户李嫣分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。