2018广东八年级下学期北师大版初中数学月考试卷131077
初中
整体难度：中等
2018-04-07
题号
一
二
三
四
五
评分
一、选择题 (共12题)
添加该题型下试题
1.
等腰三角形一腰上的高与另一腰的夹角是50°，则这个等腰三角形的底角为（ ）
A．70° B．20° C．70°或20° D．40°或140°
难度：
知识点：与三角形有关的角
使用次数：51
【答案】
C
【解答】解：①如图1，当该等腰三角形为钝角三角形时，
∵一腰上的高与另一腰的夹角是50°，
∴底角=
（90°﹣50°）=
20°，
②如图2，当该等腰三角形为锐角三角形时，
∵一腰上的高与另一腰的夹角是50°，
∴底角= [180°﹣（90°﹣50°）]=70°．
2.
已知等腰三角形的一个角是100°，则它的顶角是（ ）
A．40° B．60° C．80° D．100°
难度：
知识点：与三角形有关的角
使用次数：50
【答案】
D【解答】解：（1）当100°角为顶角时，其顶角为100°；
（2）当100°为底角时，100°×2＞180°，不能构成三角形．
故它的顶角是100°．
3.
如图，Rt△ABC中，∠C=90°，AD平分∠BAC，交BC于点D，AB=10，S△ABD=15，则CD的长为（ ）
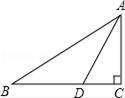
A．3 B．4 C．5 D．6
难度：
知识点：与三角形有关的线段
使用次数：108
【答案】
A【解答】解：如图，过点D作DE⊥AB于E，
∵∠C=90°，AD平分∠BAC，
∴DE=CD，
∴S△ABD=
AB•DE=×10•DE=15，
解得DE=3．
4.
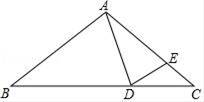
如图，在△ABC中，AB=AC，点D，E分别在边BC和AC上，若AD=AE，则下列结论错误的是（ ）
A．∠ADB=∠ACB+∠CAD B．∠ADE=∠AED
C．∠B=∠C D．∠BAD=∠BDA
难度：
知识点：与三角形有关的角
使用次数：162
【答案】
D【解答】解：∵∠ADB是△ACD的外角，
∴∠ADB=∠ACB+∠CAD，选项A
正确；
∵AD=AE，
∴∠ADE=∠AED，选项B正确；
∵AB=AC，
∴∠B=∠C，选项C正确；
∵AB≠BD，
∴∠BAD=∠BDA不成立，选项D错误；
故选：D．
5.
已知a＞b，则在下列结论中，正确的是（ ）
A．a﹣2＜b﹣2 B．﹣2a＜﹣2b C．|a|＞|b| D．a2＞b2
难度：
知识点：不等式
使用次数：105
【答案】
B【解答】解：A、∵a＞b，
∴a﹣2＞b﹣2，故此选项错误；
B、∵a＞b，∴﹣2a＜﹣2b，故此选项正确；
C、∵a＞b，∴|a|与|b|无法确定大小关系，故此选项错误；
D、∵a＞b，∴a2与b2无法确定大小关系，故此选项错误；
本卷还有19题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
24
总体难度：
中等
难度统计
难度系数
数量
占比
容易
9
37.5%
中等
15
62.5%
题型统计
大题类型
数量
占比
选择题
12
50.0%
填空题
5
20.83%
解答题
7
29.16%
知识点统计
知识点
数量
占比
与三角形有关的角
3
12.5%
与三角形有关的线段
4
16.66%
不等式
2
8.33%
一元一次不等式
3
12.5%
画轴对称图形
2
8.33%
课题学习 选择方案
4
16.66%
一元一次不等式组
2
8.33%
消元 解二元一次方程组
1
4.16%
等腰三角形
1
4.16%
三角形全等的判定
1
4.16%
勾股定理
1
4.16%
版权提示
该作品由: 用户姜德耀分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。