2017山东七年级上学期人教版初中数学期末考试129194
初中
整体难度：中等
2017-11-23
题号
一
二
三
四
五
评分
一、选择题 (共15题)
添加该题型下试题
1.
实数1，﹣1，0，﹣
四个数中，最大的数是（ ）
A．0 B．1 C．﹣1 D．
难度：
知识点：有理数
使用次数：184
【答案】
B
【考点】有理数大小比较．
【分析】根据正数大于0，0大于负数，正数大于一切负数，两负数比较大小时，绝对值大的反而小，即可解答．
【解答】解：﹣1＜﹣
＜0＜1，
故选B．
【点评】本题主要考查有理数的比较大小，解决此题问题时，特别要注意：两负数比较大小时，绝对值大的反而小．
2.
下列判断正确的是（ ）
A．3a2b与ba2不是同类项 B．
不是整式
C．单项式﹣x3y2的系数是﹣1 D．3x2﹣y+5xy2是二次三项式
难度：
知识点：整式
使用次数：130
【答案】
C【考点】同类项；整式；多项式．
【分析】分别根据单项式、多项式、整式及同类项的定义判断各选项即可．
【解答】解：A、3a2b与ba2是同类项，故本选项错误；
B、
是整式，故本选项错误；
C、单项式﹣x3y2的系数是﹣1，故本选项正确；
D、3x2﹣y+5xy2是二次三项式，故本选项错误．
故选C．
【点评】本题考查单项式、多项式、整式及同类项的定义，注意掌握单项式是数或字母的积组成的式子；单项式和多项式统称为整式．
3.
如图，两个直角∠AOB，∠COD有相同的顶点O，下列结论：①∠AOC=∠BOD；②∠AOC+∠BOD=90°；③若OC平分∠AOB，则OB平分∠COD；④∠AOD的平分线与∠COB的平分线是同一条射线．其中正确的个数有（ ）
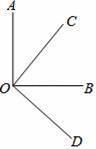
A．1个 B．2个 C．3个 D．4个
难度：
知识点：角
使用次数：50
【答案】
C【考点】角平分线的定义．
【分析】根据角的计算和角平分线性质，对四个结论逐一进行计算即可．
【解答】解：①∵∠AOB=∠COD=90°，
∴∠AOC=90°﹣∠BOC，∠BOD=90°﹣∠BOC，
∴∠AOC=∠BOD，∴①正确；
②∵只有当OC，OB分别为∠AOB和∠COD的平分线时，∠AOC+∠BOD=90°，∴②错误；
③∵∠AOB=∠COD=90°，OC平分∠AOB，
∴∠AOC=∠COB=45°，则∠BOD=90°﹣45°=45°
∴OB平分∠COD，∴③正确；
④∵∠AOB=∠COD=90°，∠AOC=∠BOD（已证）；
∴∠AOD的平分线与∠COB的平分线是同一条射线，∴④正确；
故选C．
【点评】此题主要考查学生对角的计算，角平分线的理解和掌握，此题难度不大，属于基础题．
4.
已知线段MN=10cm，点C是直线MN上一点，NC=4cm，若P是线段MN的中点，Q是线段NC的中点，则线段PQ的长度是（ ）
A．7cm B．7cm或3cm C．5cm D．3cm
难度：
知识点：直射、射线、线段
使用次数：90
【答案】
B【考点】两点间的距离．
【分析】根据线段中点的性质，可得PN，QN，根据线段的和差，可得答案．
【解答】解：P是线段MN的中点，Q是线段NC的中点，得
PN=MN=×10=5cm，QN=NC=×4=2cm．
①当C在MN上时，如图1
，
PQ=PN﹣QN=5﹣2=3cm；
②当C在MN的延长线上时如图2
，
PQ=PN+QN=5+2=7cmm，
③点C在MN的反向延长线上，NC＜MN，不成立，
故选：B．
【点评】本题考查了两点间的距离，分类讨论是解题关键，以防遗漏．
5.
如图，若A是实数a在数轴上对应的点，则关于a，﹣a，1的大小关系表示正确的是（ ）
A．a＜1＜﹣a B．a＜﹣a＜1 C．1＜﹣a＜a D．﹣a＜a＜1
难度：
知识点：有理数
使用次数：191
【答案】
A【考点】实数与数轴．
【分析】根据数轴可以得到a＜1＜﹣a，据此即可确定哪个选项正确．
【解答】解：∵实数a在数轴上原点的左边，
∴a＜0，但|a|＞1，﹣a＞1，
则有a＜1＜﹣a．
故选A．
【点评】本题考查了实数与数轴的对应关系，数轴上的数右边的数总是大于左边的数
本卷还有18题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
23
总体难度：
中等
难度统计
难度系数
数量
占比
容易
15
65.21%
中等
8
34.78%
题型统计
大题类型
数量
占比
选择题
15
65.21%
填空题
4
17.39%
计算题
2
8.69%
解答题
2
8.69%
知识点统计
知识点
数量
占比
有理数
3
13.04%
整式
2
8.69%
角
2
8.69%
直射、射线、线段
2
8.69%
从算式到方程
3
13.04%
实际问题与一元一次方程
3
13.04%
有理数的乘方
5
21.73%
整式的加减
1
4.34%
解一元一次方程（二）去括号与去分母
2
8.69%
版权提示
该作品由: 用户高国营分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。