2017甘肃九年级上学期人教版初中数学期中考试128460
初中
整体难度：中等
2017-10-08
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
下列方程是一元二次方程的是（ ）
A．x2+2x﹣3 B．x2+3=0 C．（x2+3）2=9 D．
难度：
知识点：一元二次方程
使用次数：122
【答案】
B
【考点】一元二次方程的定义．
【分析】本题根据一元二次方程的定义求解．
一元二次方程必须满足三个条件：
（1）是整式方程；
（2）含有一个未知数，且未知数的最高次数是2；
（3）二次项系数不为0．
以上三个条件必须同时成立，据此即可作出判断．
【解答】解：A、不是方程，错误；
B、符合一元二次方程的定义，正确；
C、原式可化为x4+6x2=0，是一元四次方程，错误；
D、是分式方程，错误．
故选B．
【点评】在做此类判断题时，要特别注意二次项系数a≠0这一条件．
2.
用配方法解一元二次方程x2﹣4x=5时，此方程可变形为（ ）
A．（x+2）2=1 B．（x﹣2）2=1 C．（x+2）2=9 D．（x﹣2）2=9
难度：
知识点：解一元二次方程
使用次数：160
【答案】
D【考点】解一元二次方程-配方法．
【专题】配方法．
【分析】配方法的一般步骤：
（1）把常数项移到等号的右边；
（2）把二次项的系数化为1；
（3）等式两边同时加上一次项系数一半的平方．
选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
【解答】解：∵x2﹣4x=5，∴x2﹣4x+4=5+4，∴（x﹣2）2=9．故选D．
【点评】此题考查了配方法解一元二次方程，解题时要注意解题步骤的准确应用．
3.
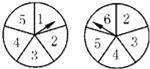
如图所示的两个圆盘中，指针落在每一个数上的机会均等，那么两个指针同时落在偶数上的概率是（ ）
A．
B．
C．
D．
难度：
知识点：随机事件与概率
使用次数：109
【答案】
C【考点】列表法与树状图法．
【分析】列举出所有情况，看两个指针同时落在偶数上的情况数占总情况数的多少即可．
【解答】解：列表得：
| （1，6） | （2，6） | （3，6） | （4，6） | （5，6） |
| （1，5） | （2，5） | （3，5） | （4，5） | （5，5） |
| （1，4） | （2，4） | （3，4） | （4，4） | （5，4） |
| （1，3） | （2，3） | （3，3） | （4，3） | （5，3） |
| （1，2） | （2，2） | （3，2） | （4，2） | （5，2） |
∴一共有25种情况，两个指针同时落在偶数上的有6种情况，
∴两个指针同时落在偶数上的概率是
．
故选C．
【点评】列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；用到的知识点为：概率=所求情况数与总情况数之比．
4.
下列给出的条件中，能判断四边形ABCD是平行四边形的是（ ）
A．AB∥CD，AD=BC B．∠B=∠C；∠A=∠D C．AB=AD，CB=CD D．AB=CD，AD=BC
难度：
知识点：平行四边形
使用次数：111
【答案】
D【考点】平行四边形的判定．
【分析】直接利用平行四边形的判定定理求解即可求得答案．注意掌握排除法在选择题中的应用．
【解答】解：A、∵AB∥CD，AD=BC，
∴四边形ABCD是平行四边形或梯形；故本选项错误；
B、由∠B=∠C，∠A=∠D，不能四边形ABCD是平行四边形；故本选项错误；
C、由AB=AD，CB=CD，不能判断四边形ABCD是平行四边形；
故本选项错误；
D、∵AB=CD，AD=BC，
∴四边形ABCD是平行四边形；故本选项正确．
故选D．
【点评】此题考查了平行四边形的判定．注意掌握举反例的解题方法是关键．
5.
下列识别图形不正确的是（ ）
A．有一个角是直角的平行四边形是矩形
B．有三个角是直角的四边形是矩形
C．对角线相等的四边形是矩形
D．对角线互相平分且相等的四边形是矩形
难度：
知识点：特殊的平行四边形
使用次数：129
【答案】
C【考点】矩形的判定．
【专题】证明题．
【分析】矩形的判定定理有：
（1）有一个角是直角的平行四边形是矩形．
（2）有三个角是直角的四边形是矩形．
（3）对角线互相平分且相等的四边形是矩形，据此判定．
【解答】解：A、有一个角是直角的平行四边形是矩形，正确；
B、有三个角是直角的四边形是矩形，正确；
C、对角线相等的四边形不一定是矩形，对角线相等的平行四边形才是矩形，错误；
D、对角线互相平分且相等的四边形是矩形，正确．
故选C．
【点评】本题主要考查的是矩形的判定定理．
（1）有一个角是直角的平行四边形是矩形．
（2）有三个角是直角的四边形是矩形．
（3）对角线互相平分且相等的四边形是矩形，据此判定．
本卷还有26题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
31
总体难度：
中等
难度统计
难度系数
数量
占比
容易
15
48.38%
中等
16
51.61%
题型统计
大题类型
数量
占比
选择题
10
32.25%
填空题
11
35.48%
计算题
4
12.90%
解答题
6
19.35%
知识点统计
知识点
数量
占比
一元二次方程
2
6.45%
解一元二次方程
9
29.03%
随机事件与概率
1
3.22%
平行四边形
4
12.90%
特殊的平行四边形
3
9.67%
相似三角形
5
16.12%
实际问题与一元二次方程
3
9.67%
图形的相似
1
3.22%
用频率估计概率
1
3.22%
位似
1
3.22%
用列举法求概率
1
3.22%
版权提示
该作品由: 用户yining分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。