2017江苏苏科版初中数学期末考试127882
初中
整体难度：中等
2017-09-03
题号
一
二
三
四
五
评分
一、解答题 (共9题)
添加该题型下试题
1.
观察下列关于自然数的等式：
a1：32-12=8×1；
a2：52-32=8×2；
a3：72-52=8×3；……
根据上述规律解决下列问题：
（1）写出第a4个等式：___________；
（2）写出你猜想的第an个等式（用含n的式子表示），并验证其正确性；
（3）对于正整数k，若ak，ak+1，ak+2为△ABC的三边，求k的取值范围．
难度：
知识点：乘法公式
使用次数：185
【答案】
（1）a4应为92—72=8×4（2分）；（2）规律：（2n+1)2-（2n-1)2=8n（n为正整数）（4分，不写“n为正整数”不扣分）.验证：（2n+1)2-（2n-1)2＝[(2n+1)+（2n-1)] [(2n+1)-（2n-1)] =4n×2=8n（6分）；（3）由（2）可知，ak=8k，ak+1=8（k+1），ak+2=8（k+2）（9分），易知8k<8（k+1）<8（k+2），要使它们能构成一个三角形，则必须有8k+8（k+1）>8（k+2）（11分），解得k>1．所以k的取值范围是k>1且k为正整数（12分）
2.
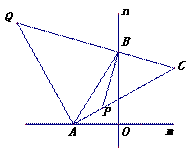
如图，直线m与直线n互相垂直，垂足为O,A、B两点同时从点O出发，点A沿直线m向左运动，点B沿直线n向上运动.
（1）若∠BAO和∠ABO的平分线相交于点P，
在点A、B的运动过程中，∠APB的大
小是否会发生变化？若不发生变化，请
求出其值；若发生变化，请说明理由；
（2）若∠ABO的两个外角的平分线AQ、BQ相
交于点Q，AP的延长线交QB的延长线于
点C，在点A、B的运动过程中，∠Q和
∠C的大小是否会发生变化？若不发生变 （第24题图）
化，请求出∠Q和∠C的度数；若发生变
化，请说明理由.
难度：
知识点：相交线
使用次数：57
【答案】
（1）不变化（1分）.理由：∵AP和BP分别是∠BAO和∠ABO的平分线，∠AOB=90°，∴∠APB=180°-
（∠OAB+ABO）=180°-×90°=135°（5分）；（2）都不变（6分）.理由：∵AQ和BQ分别是∠BAO的邻补角和∠ABO的邻补角的平分线，AP和BP分别是∠BAO和∠ABO的平分线，∴∠CAQ=∠QBP=90°，又∠APB=135°，∴∠Q=45°，∴∠C=45°（10分）.
3.
已知关于x、y的方程组
（1）求方程组的解（用含m的代数式表示）； （第22题图）
（2）若方程组的解满足条件x＜0，且y＜0，求m的取值范围．
难度：
知识点：消元 解二元一次方程组
使用次数：115
【答案】
（1）
（5分，求出x、y各2分，方程组的解1分）；
（2）根据题意，得
（7分），m＜-8（10分）.
4.
如图，△ABC中，AB＝AC，AD⊥BC，
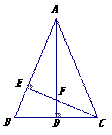CE⊥AB，AE＝CE．求证：
（1）△AEF≌△CEB；
（2）AF＝2CD．
难度：
知识点：三角形全等的判定
使用次数：171
【答案】
(1)∵AD⊥BC，CE⊥AB，∴∠AEF=∠CEB=∠ADC=90°，即 ∠AFE+
∠EAF=∠CFD+∠ECB=90°.又∵∠AFE=∠CFD,∴∠EAF=∠ECB(3分).在△AEF和△CEB中，∠AEF=∠CEB，AE=CE，∠EAF=∠ECB,∴△AEF≌△CEB(5分)；(2)由△AEF≌△CEB，可得AF=BC(6分).又∵AD⊥BC，∴∠ADB=∠ADC=90°.在Rt△ABD和Rt△ACD中
∵AB=AC，AD=AD，∴Rt△ABD≌Rt△ACD（HL），∴CD=BD，∴BC=2CD，∴AF=2CD(10分)（直接用“三线合一”扣3分）
5.
学校准备购进一批节能灯，已知1只A型节能灯和3只B型节能灯共需26元；3只A型节能灯和2只B型节能灯共需29元.2
（1）求一只A型节能灯和一只B型节能灯的售价各是多少元；
（2）学校准备购进这两种型号的节能灯共50只，并且A型节能灯的数量不多
于B型节能灯数量的3倍，问A型节能灯最多可以买多少只？
难度：
知识点：实际问题与二元一次方程组
使用次数：182
【答案】
（1）设一只A型节能灯的售价是
元，一只B型节能灯的售价是
元（1分）. 依题意得
（3分），解得
（4分）.答;一只A型节能灯的售价是5元，一只B型节能灯的售价是7元（5分）；（2）设购进A型节能灯
只，则购进B型节能灯（50-m）只 ，依题意有
（8分），解得
（9分）.∵m是正整数，∴m=37.答：A型节能灯最多购进37只（10分）
本卷还有23题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
28
总体难度：
中等
难度统计
难度系数
数量
占比
中等
18
64.28%
容易
10
35.71%
题型统计
大题类型
数量
占比
解答题
9
32.14%
计算题
3
10.71%
填空题
10
35.71%
选择题
6
21.42%
知识点统计
知识点
数量
占比
乘法公式
3
10.71%
相交线
1
3.57%
消元 解二元一次方程组
1
3.57%
三角形全等的判定
4
14.28%
实际问题与二元一次方程组
1
3.57%
角
1
3.57%
不等式
4
14.28%
因式分解
3
10.71%
整式的乘法
4
14.28%
分式的运算
2
7.14%
一元一次不等式组
2
7.14%
实际问题与一元一次方程
1
3.57%
二元一次方程组
1
3.57%
版权提示
该作品由: 用户吕书洋分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。