在平面直角坐标系![]() 中的点
中的点![]() 和图形
和图形![]() ,给出如下的定义:若在图形
,给出如下的定义:若在图形![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 两点间的距离小于或等于1,则称
两点间的距离小于或等于1,则称![]() 为图形
为图形![]() 的关联点.
的关联点.
(1)当![]() 的半径为2时,
的半径为2时,
①在点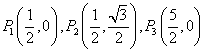 中,
中,![]() 的关联点
的关联点![]() 是_______________.
是_______________.
②点![]() 在直线
在直线![]() 上,若
上,若![]() 为
为![]() 的关联点,求点
的关联点,求点![]() 的横坐标的取值范围.
的横坐标的取值范围.
(2)![]() 的圆心在
的圆心在![]() 轴上,半径为2,直线
轴上,半径为2,直线![]() 与
与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() .若线段
.若线段![]() 上的所有点都是
上的所有点都是![]() 的关联点,直接写出圆心
的关联点,直接写出圆心![]() 的横坐标的取值范围.
的横坐标的取值范围.
试题解析:
(1)![]() ,
,
点![]() 与⊙的最小距离为
与⊙的最小距离为![]() ,点
,点![]() 与⊙的最小距离为1,点
与⊙的最小距离为1,点![]() 与⊙的最小距离为
与⊙的最小距离为![]() ,
,
∴⊙的关联点为![]() 和
和![]() .
.
②根据定义分析,可得当直线y=-x上的点P到原点的距离在1到3之间时符合题意;
∴ 设点P的坐标为P (x ,-x) ,
当OP=1时,由距离公式可得,OP=![]() ,解得
,解得![]() ,当OP=3时,由距离公式可得,OP=
,当OP=3时,由距离公式可得,OP=![]() ,
,![]() ,解得
,解得![]() ,
,
∴ 点的横坐标的取值范围为-![]() ≤x≤-
≤x≤-![]() 或
或![]() ≤x≤
≤x≤![]()
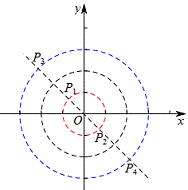

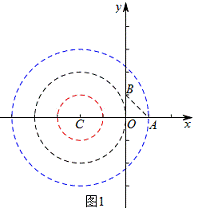
如图2,当圆与小圆相切时,切点为D,
∴CD=1 ,
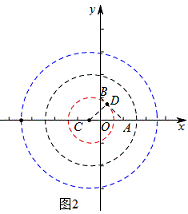

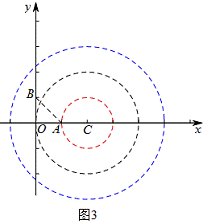
如图3,当圆过点A时,AC=1,
C点坐标为(2,0)
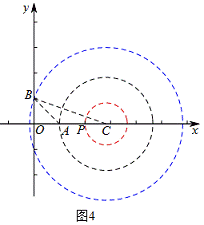
如图4,
当圆过点 B 时,连接 BC ,此时 BC =3,
在 Rt△OCB中,由勾股定理得OC=![]() , C点坐标为 (2
, C点坐标为 (2![]() ,0).
,0).
∴ C![]() 点的横坐标的取值范围为2≤
点的横坐标的取值范围为2≤![]() ≤2
≤2![]() ;
;
∴综上所述点C的横坐标的取值范围为-![]() ≤
≤![]() ≤-
≤-![]() 或
或![]() ≤
≤![]() ≤
≤![]() .
.
在等腰直角![]() 中,
中,![]() ,
,![]() 是线段
是线段![]() 上一动点(与点
上一动点(与点![]() 不重合),连接
不重合),连接![]() ,延长
,延长![]() 至点
至点![]() ,使得
,使得![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)用等式表示线段![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
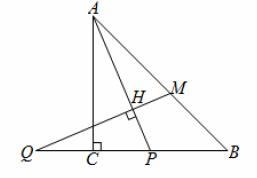

(1) ∠AMQ=45°+![]() .理由如下:
.理由如下:
∵∠PAC=![]() ,△ACB是等腰直角三角形, ∴∠PAB=45°-
,△ACB是等腰直角三角形, ∴∠PAB=45°-![]() ,∠AHM=90°,∴∠AMQ=180°-∠AHM-∠PAM=45°+
,∠AHM=90°,∴∠AMQ=180°-∠AHM-∠PAM=45°+![]() .
.
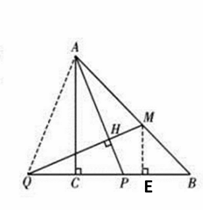
(2)线段MB与PQ之间的数量关系:PQ=![]() MB.
MB.
理由如下:
连接AQ,过点M做ME⊥QB,
∵AC⊥QP,CQ=CP, ∴∠QAC=∠PAC=![]() ,∴∠QAM=
,∴∠QAM=![]() +45°=∠AMQ, ∴AP=AQ=QM,在RT△APC和RT△QME中,
+45°=∠AMQ, ∴AP=AQ=QM,在RT△APC和RT△QME中,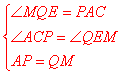 ∴RT△APC≌RT△QME, ∴PC=ME, ∴△MEB是等腰直角三角形,∴
∴RT△APC≌RT△QME, ∴PC=ME, ∴△MEB是等腰直角三角形,∴![]() ,
,
∴PQ=![]() MB.
MB.
考点:全等三角形判定,等腰三角形性质 .
在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的表达式;
的表达式;
(2)垂直于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() ,结合函数的图象,求
,结合函数的图象,求![]() 的取值范围.
的取值范围.

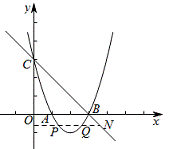
(2).由![]() ,∴抛物线的顶点坐标为(2,-1),对称轴为直线x=2, ∵
,∴抛物线的顶点坐标为(2,-1),对称轴为直线x=2, ∵![]() ,∴
,∴![]() +
+![]() =4.令y=-1,y=-x+3,x=4. ∵
=4.令y=-1,y=-x+3,x=4. ∵ ![]() ,∴3<
,∴3<![]() <4, 即7<
<4, 即7<![]() <8, ∴
<8, ∴ ![]() 的取值范围为:7<
的取值范围为:7<![]() <8.
<8.
考点:二次函数与x轴的交点问题,待定系数法求函数解析式,二次函数的对称性.
如图,![]() 是
是![]() 所对弦
所对弦![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .(当点
.(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为0)
的值为0)
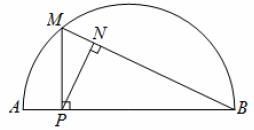
小东根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
| 0 | 2.0 | 2.3 | 2.1 | 0.9 | 0 |
(说明:补全表格时相关数值保留一位小数)
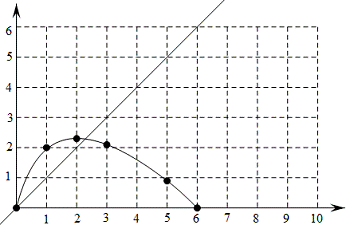
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度约为____________
的长度约为____________![]() .
.
试题解析:(1)1.6
(2)如图所示:
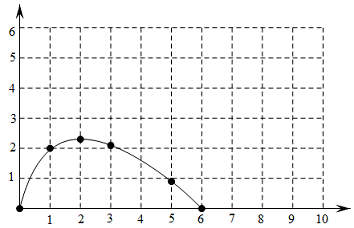
(3)作y=x与函数图象交点即为所求.2.2(答案不唯一)
考点:函数图象,估算,近似数
某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
| 成绩 人数 部门 |
|
|
|
|
|
|
| 甲 | 0 | 0 | 1 | 11 | 7 | 1 |
| 乙 |
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
| 部门 | 平均数 | 中位数 | 众数 |
| 甲 | 78.3 | 77.5 | 75 |
| 乙 | 78 | 80.5 | 81 |
得出结论:
![]() .估计乙部门生产技能优秀的员工人数为____________;
.估计乙部门生产技能优秀的员工人数为____________;
![]() .可以推断出_____________部门员工的生产技能水平较高,理由为_____________.(至少从两个不同的角度说明推断的合理性)
.可以推断出_____________部门员工的生产技能水平较高,理由为_____________.(至少从两个不同的角度说明推断的合理性)

按如下分数段整理 按如下分数段整理数据:
| 成绩 人数 部门 |
|
|
|
|
|
|
| 甲 | 0 | 0 | 1 | 11 | 7 | 1 |
| 乙 | 1 | 0 | 0 | 7 | 10 | 2 |
a.估计乙部门生产技能优秀的员工人数为400×![]() =240(人);
=240(人);
b.答案不唯一,言之有理即可.
可以推断出甲部门员工的生产技能水平较高,理由如下:
①甲部门生产技能测试中,测试成绩的平均数较高,表示甲部门生产技能水平较高;
②甲部门生产技能测试![]() 中,没有生产技能不合格的员工.
中,没有生产技能不合格的员工.
可以推断出乙部门员工的生产技能水平较高,理由如下:
①乙部门生产技能测试中,测试成绩的中位数较高,表示乙部门生产技能水平优秀的员工较多;
②乙部门生产技能测试中,测试成绩的众数较高,表示乙部门生产技能水平较高.
考点:众数,中位数.
本卷还有24题,登录并加入会员即可免费使用哦~

该作品由: 用户小王子分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。