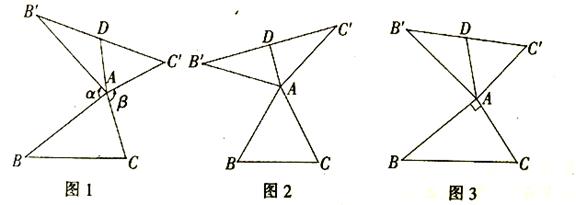
我们定义:如图1,在![]() 看,把
看,把![]() 点
点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .当
.当![]() 时,我们称
时,我们称![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”, ![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.
叫做“旋补中心”.
特例感知:
(1)在图2,图3中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”, ![]() 是
是![]() 的“旋补中心”.
的“旋补中心”.
①如图2,当![]() 为等边三角形时,
为等边三角形时,![]() 与
与![]() 的数量关系为
的数量关系为![]() _____________
_____________![]() ;
;
②如图3,当![]() 时,则
时,则![]() 长为_________________.
长为_________________.
猜想论证:
(2)在图1中,当![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.
拓展应用
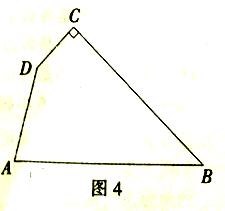
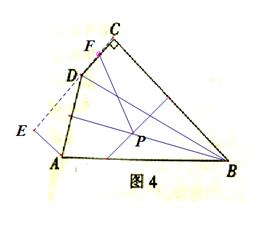
(3)如图4,在四边形![]() ,
,![]() ,
,![]() .在四边形内部是否存在点
.在四边形内部是否存在点![]() ,使
,使![]() 是
是![]() 的“旋补三角形”?若存在,给予证明,并求
的“旋补三角形”?若存在,给予证明,并求![]() 的“旋补中线”长;若不存在,说明理由.2·1·c·n·j·y
的“旋补中线”长;若不存在,说明理由.2·1·c·n·j·y
(1)在图2,图3中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”, ![]() 是
是![]() 的“旋补中线”.
的“旋补中线”.
①如图2,当![]() 为等边三角形时,
为等边三角形时,![]() 与
与![]() 的数量关系为
的数量关系为![]() ______
______![]() _______
_______![]() ;
;
②如图3,当![]() 时,则
时,则![]() 长为________4_________.
长为________4_________.
猜想论证:
(2)
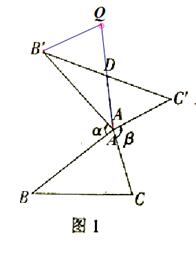
解(2)猜想![]()
解题过程:如图,将三角形![]() 绕点D逆时针旋转,使DC与
绕点D逆时针旋转,使DC与![]() 重合,证明
重合,证明![]()
拓展应用
(3)

已知抛物线![]() .
.
(1)当![]() 时,求抛物线与
时,求抛物线与![]() 轴的交点坐标及对称轴;
轴的交点坐标及对称轴;
(2)①试说明无论![]() 为何值,抛物线
为何值,抛物线![]() 一定经过两个定点,并求出这两个定点的坐标;
一定经过两个定点,并求出这两个定点的坐标;
②将抛物线![]() 沿这两个定点所在直线翻折,得到抛物线
沿这两个定点所在直线翻折,得到抛物线![]() ,直接写出
,直接写出![]() 的表达式;
的表达式;
(3)若(2)中抛物线![]() 的顶点到
的顶点到![]() 轴的距离为2,求
轴的距离为2,求![]() 的值.
的值.

已知抛物线![]() .
.

如图1,![]() 的直径
的直径![]() 是弦
是弦![]() 上一动点(与点
上一动点(与点![]() 不重合),
不重合),![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
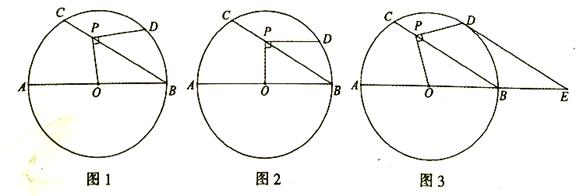
(1)如图2,当![]() 时,求
时,求![]() 的长;
的长;
(2)如图3,当![]() 时,延长
时,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
①求证:![]() 是
是![]() 的切线;
的切线;
②求![]() 的长.
的长.

如图,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .已知点
.已知点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 方向平移,使点
方向平移,使点![]() 移动到点
移动到点![]() ,得到
,得到![]() .过点
.过点![]() 作
作![]() 轴交双曲线于点
轴交双曲线于点![]() .w
.w
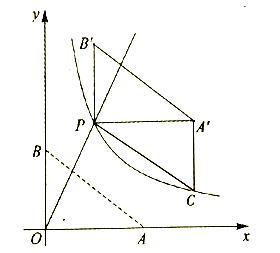
(1)求![]() 与
与![]() 的值;
的值;
(2)求直线![]() 的表达式;
的表达式;
(3)直接写出线段![]() 扫过的面积.
扫过的面积.

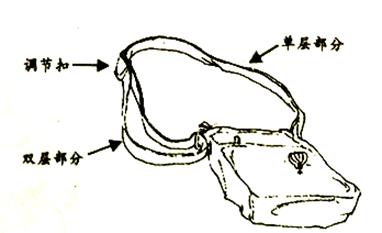
如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为![]() ,双层部分的长度为
,双层部分的长度为![]() ,经测量,得到如下数据:
,经测量,得到如下数据:
| 单层部分的长度
| … | 4 | 6 | 8 | 10 | … | 150 |
| 双层部分的长度 | … | 73 | 72 | 71 | … |
(1)根据表中数据的规律,完成以下表格,并直接写出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)根据小敏的身高和习惯,挎带的长度为![]() 时,背起来正合适,请求出此时单层部分的长度;
时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为![]() ,求
,求![]() 的取值范围.
的取值范围.

本卷还有19题,登录并加入会员即可免费使用哦~

该作品由: 用户瑞士糖分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。