2016内蒙古八年级上学期人教版初中数学期末考试123873
初中
整体难度：中等
2017-01-28
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
下列图案属于轴对称图形的是( )
A．
B．
C．
D．
难度：
知识点：轴对称
使用次数：164
【答案】
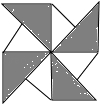
C
【考点】轴对称图形．
【分析】根据轴对称图形的概念求解．
【解答】解：根据轴对称图形的概念知A、B、D都不是轴对称图形，只有C是轴对称图形．故选C．
【点评】轴对称图形的判断方法：把某个图象沿某条直线折叠，如果图形的两部分能够重合，那么这个是轴对称图形．
2.
下列计算正确的是( )
A．（a3）2=a5 B．a2+a5=a7 C．（ab）3=ab3 D．a2•a5=a7
难度：
知识点：整式的乘法
使用次数：100
【答案】
D【考点】幂的乘方与积的乘方；合并同类项；同底数幂的乘法．
【分析】直接利用幂的乘方运算法则以及合并同类项法则、积的乘方运算法则分别化简求出答案．
【解答】解：A、（a3）2=a6，故此选项错误；
B、a2+a5无法进行计算，故此选项错误；
C、（ab）3=a3b3，故此选项错误；
D、a2•a5=a7，正确；
故选：D．
【点评】此题主要考查了幂的乘方运算以及合并同类项、积的乘方运算等知识，正确掌握运算法则是解题关键．
3.
已知三角形两边长分别为7、11，那么第三边的长可以是( )
A．2 B．3 C．4 D．5
难度：
知识点：与三角形有关的线段
使用次数：137
【答案】
D【考点】三角形三边关系．
【分析】根据三角形的三边关系可得11﹣7＜第三边长＜11+7，再解可得第三边的范围，然后可得答案．
【解答】解：设第三边长为x，由题意得：
11﹣7＜x＜11+7，
解得：4＜x＜18，
故选：D．
【点评】此题主要考查了三角形的三边关系，关键是掌握三角形两边之和大于第三边，三角形的两边差小于第三边．
4.
如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是( )
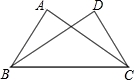
A．∠A=∠D B．AB=DC C．∠ACB=∠DBC D．AC=BD
难度：
知识点：三角形全等的判定
使用次数：193
【答案】
D【考点】全等三角形的判定．
【分析】根据题目所给条件∠ABC=∠DCB，再加上公共边BC=BC，然后再结合判定定理分别进行分析即可．
【解答】解：A、添加∠A=∠D可利用AAS判定△ABC≌△DCB，故此选项不合题意；
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB，故此选项不合题意；
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB，故此选项不合题意；
D、添加AC=BD不能判定△ABC≌△DCB，故此选项符合题意；
故选：D．
【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
5.
若分式
有意义，则x的取值范围是( )
A．x≠0 B．
C．
D．
难度：
知识点：分式
使用次数：158
【答案】
B【考点】分式有意义的条件．
【分析】根据分式有意义的条件可得1﹣2x≠0，再解即可．
【解答】解：由题意得：1﹣2x≠0，
解得：x≠
，
故选：B．
【点评】此题主要考查了分式有意义的条件，关键是掌握分式有意义的条件是分母不等于零．
本卷还有22题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
27
总体难度：
中等
难度统计
难度系数
数量
占比
中等
12
44.44%
容易
13
48.14%
偏难
2
7.40%
题型统计
大题类型
数量
占比
选择题
10
37.03%
填空题
8
29.62%
计算题
3
11.11%
解答题
5
18.51%
综合题
1
3.70%
知识点统计
知识点
数量
占比
轴对称
3
11.11%
整式的乘法
3
11.11%
与三角形有关的线段
1
3.70%
三角形全等的判定
4
14.81%
分式
1
3.70%
与三角形有关的角
1
3.70%
分式方程
4
14.81%
因式分解
2
7.40%
分式的运算
2
7.40%
等腰三角形
2
7.40%
多边形及其内角相和
1
3.70%
有理数的乘除法
1
3.70%
画轴对称图形
2
7.40%
版权提示
该作品由: 用户胡常委分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。