2016九年级上学期北师大版初中数学同步练习122290
初中
整体难度：中等
2016-11-16
题号
一
二
三
四
五
评分
一、选择题 (共6题)
添加该题型下试题
1.
矩形、菱形、正方形都具有的性质是( )
A．每一条对角线平分一组对角
B．对角线相等
C．对角线互相平分
D．对角线互相垂直
难度：
知识点：特殊的平行四边形
使用次数：172
【答案】
C
2.
已知O为四边形ABCD对
角线的交点，下列条件能使四边形ABCD成为矩形的是( )
A．OA＝OC，OB＝OD
B．AC＝BD
C．AC⊥BD
D．∠ABC＝∠BCD＝∠CDA＝90°
难度：
知识点：特殊的平行四边形
使用次数：178
【答案】
D
3.
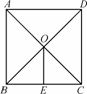
如图，已知在正方形ABCD中，对角线AC与BD相交于点O，O
E∥AB交BC于点E，若AD＝8 cm，则OE的长为( )
A．3 cm B．4 cm
C．6 cm D．
8 cm
难度：
知识点：特殊的平行四边形
使用次数：180
【答案】
B
4.
四边形ABCD的对角线AC，BD相交于点O，能判定它为正方形的条件是( )
A．AO＝CD
B．AO＝CO＝BO＝DO
C．AO＝CO，BO＝DO，AC⊥BD
D．AO＝BO＝CO＝DO，AC⊥BD
难度：
知识点：特殊的平行四边形
使用次数：178
【答案】
.D
5.
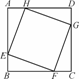
如图，正方形ABCD的边长为8，在各边上顺次截取AE＝BF＝CG＝DH＝5，则四边形EFGH的面积是( )
A．30 B．34
C．36 D．40
难度：
知识点：特殊的平行四边形
使用次数：110
【答案】
B
本卷还有8题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
13
总体难度：
中等
难度统计
难度系数
数量
占比
中等
7
53.84%
容易
5
38.46%
基础
1
7.69%
题型统计
大题类型
数量
占比
选择题
6
46.15%
填空题
4
30.76%
解答题
3
23.07%
知识点统计
知识点
数量
占比
特殊的平行四边形
13
100.0%
版权提示
该作品由: 用户feng分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。