2016湖北八年级下学期人教版初中数学期中考试121417
初中
整体难度：中等
2016-10-06
题号
一
二
三
四
五
评分
一、选择题 (共7题)
添加该题型下试题
1.
下列式子中，属于最简二次根式的是（ ）
A．
B．
C．
D．
难度：
知识点：二次根式
使用次数：197
【答案】
B【考点】最简二次根式．
【专题】计算题．
【分析】判断一个二次根式是否为最简二次根式主要方法是根据最简二次根式的定义进行，或直观地观察被开方数的每一个因数（或因式）的指数都小于根指数2，且被开方数中不含有分母，被开方数是多项式时要先因式分解后再观察．
【解答】解：A、
=3，故A错误；
B、
是最简二次根式，故B正确；
C、
=2
，不是最简二次根式，故C错误；
D、
=
，不是最简二次根式，故D错误；
故选：B．
【点评】本题考查了最简二次根式的定义．在判断最简二次根式的过程中要注意：
（1）被开方数不含分母；
（2）被开方数不含能开得尽方的因数或因式．
2.
下列式子没有意义的是（ ）
A．
B．
C．
D．
难度：
知识点：二次根式
使用次数：114
【答案】
A【考点】二次根式有意义的条件．
【分析】根据二次根式的被开方数是非负数，可得答案．
【解答】解：A、
没有意义，故A符合题意；
B、
有意义，故B不符合题意；
C、
有意义，故C不符合题意；
D、
有意义，故D不符合题意；
故选：A．
【点评】本题考查了二次根式有意义的条件，二次根式的被开方数是非负数是解题关键．
3.
下列计算正确的有（ ）
A．
+
=
B．2
﹣=2 C．
×=
D．
=2
难度：
知识点：二次根式的乘除
使用次数：181
【答案】
C【考点】二次根式的混合运算．
【专题】计算题．
【分析】根据二次根式的加减法对A、B进行判断；根据二次根式的乘法法则对C进行判断；根据二次根式的性质对D进行判断．
【解答】解：A、
与
不能合并，所以A选项错误；
B、原式=2
，所以B选项错误；
C、原式=
=
，所以C选项正确；
D、原式=
，所以D选项错误．
故选C．
【点评】本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．
4.
适合下列条件的△ABC中，直角三角形的个数为（ ）
①a=3，b=4，c=5；
②a=6，∠A=45°；
③a=2，b=2，c=2
；
④∠A=38°，∠B=52°．
A．1个 B．2个 C．3个 D．4个
难度：
知识点：勾股定理的逆定理
使用次数：118
【答案】
C【考点】勾股定理的逆定理．
【分析】根据勾股定理的逆定理以及直角三角形的定义，验证四组条件中数据是否满足“较小两边平方的和等于最大边的平方”或“有一个角是直角”，由此即可得出结论．
【解答】解：①a=3，b=4，c=5，
∵32+42=25=52，
∴满足①的三角形为直角三角形；
②a=6，∠A=45°，
只此两个条件不能断定三角形为直角三角形；
③a=2，b=2，c=2
，
∵22+22=8=
，
∴满足③的三角形为直角三角形；
④∵∠A=38°，∠B=52°，
∴∠C=180°﹣∠A﹣∠B=90°，
∴满足④的三角形为直角三角形．
综上可知：满足①③④的三角形均为直角三角形．
故选C．
【点评】本题考查了勾股定理的逆定理以及直角三角形的定义，解题的关键是根据勾股定理的逆定理和直角三角形的定义验证四组条件．本题属于基础题，难度不大，解决该题型题目时，套入数据验证“较小两边平方的和是否等于最大边的平方（或寻找三角形中是否有一个角为直角）”是关键．
5.
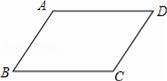
在下列给出的条件中，能判定四边形ABCD为平行四边形的是（ ）
A．AB=BC，CD=DA B．AB∥CD，AD=BC C．AB∥CD，∠A=∠C D．∠A=∠B，∠C=∠D
难度：
知识点：平行四边形
使用次数：197
【答案】
C【考点】平行四边形的判定．
【分析】根据平行四边形的判定进行判断即可得出结论．
【解答】解：如图所示，根据平行四边形的判定，A、B、D条件均不能判定为平行四边形，
C选项中，由于AB∥CD，∠A=∠C，所以∠B=∠D，
所以只有C能判定．
故选C．
【点评】平行四边形的判定方法共有五种，在四边形中如果有：
1、四边形的两组对边分别平行；
2、一组对边平行且相等；
3、两组对边分别相等；
4、对角线互相平分；
5、两组对角分别相等．则四边形是平行四边形．
本卷还有20题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
25
总体难度：
中等
难度统计
难度系数
数量
占比
容易
8
32.0%
中等
16
64.0%
偏难
1
4.0%
题型统计
大题类型
数量
占比
选择题
7
28.00%
填空题
7
28.00%
计算题
2
8.0%
解答题
9
36.0%
知识点统计
知识点
数量
占比
二次根式
6
24.0%
二次根式的乘除
2
8.0%
勾股定理的逆定理
1
4.0%
平行四边形
5
20.0%
特殊的平行四边形
5
20.0%
二次根式的加减
2
8.0%
勾股定理
4
16.0%
版权提示
该作品由: 用户彭大分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。