如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=![]()
![]() ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
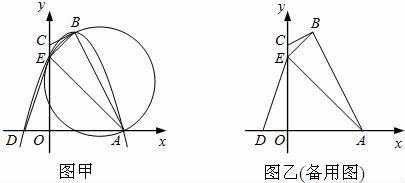

【分析】(1)已知A、D、E三点的坐标,利用待定系数法可确定抛物线的解析式,进而能得到顶点B的坐标.
(2)过B作BM⊥y轴于M,由A、B、E三点坐标,可判断出△BME、△AOE都为等腰直角三角形,易证得∠BEA=90°,即△ABE是直角三角形,而AB是△ABE外接圆的直径,因此只需证明AB与CB垂直即可.BE、AE长易得,能求出tan∠BAE的值,结合tan∠CBE的值,可得到∠CBE=∠BAE,由此证得∠CBA=∠CBE+∠ABE=∠BAE+∠ABE=90°,此题得证.
(3)△ABE中,∠AEB=90°,tan∠BAE=![]()
![]() ,即AE=3BE,若以D、E、P为顶点的三角形与△ABE相似,那么该三角形必须满足两个条件:①有一个角是直角、②两直角边满足1:3的比例关系;然后分情况进行求解即可.
,即AE=3BE,若以D、E、P为顶点的三角形与△ABE相似,那么该三角形必须满足两个条件:①有一个角是直角、②两直角边满足1:3的比例关系;然后分情况进行求解即可.
(4)过E作EF∥x轴交AB于F,当E点运动在EF之间时,△AOE与△ABE重叠部分是个四边形;当E点运动到F点右侧时,△AOE与△ABE重叠部分是个三角形.按上述两种情况按图形之间的和差关系进行求解.
【解答】(1)解:由题意,设抛物线解析式为y=a(x﹣3)(x+1).
将E(0,3)代入上式,解得:a=﹣1.
∴y=﹣x2+2x+3.
则点B(1,4).
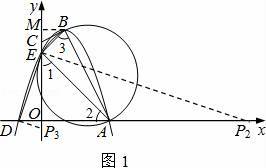
(2)证明:如图1,过点B作BM⊥y于点M,则M(0,4).
在Rt△AOE中,OA=OE=3,
∴∠1=∠2=45°,AE=![]()
![]() =3
=3![]()
![]() .
.
在Rt△EMB中,EM=OM﹣OE=1=BM,
∴∠MEB=∠MBE=45°,BE=![]()
![]() =
=![]()
![]() .
.
∴∠BEA=180°﹣∠1﹣∠MEB=90°.
∴AB是△ABE外接圆的直径.
在Rt△ABE中,tan∠BAE=![]()
![]() =
=![]()
![]() =tan∠CBE,
=tan∠CBE,
∴∠BAE=∠CBE.
在Rt△ABE中,∠BAE+∠3=90°,∴∠CBE+∠3=90°.
∴∠CBA=90°,即CB⊥AB.
∴CB是△ABE外接圆的切线.
(3)解:Rt△ABE中,∠AEB=90°,tan∠BAE=![]()
![]() ,sin∠BAE=
,sin∠BAE=![]()
![]() ,cos∠BAE=
,cos∠BAE=![]()
![]() ;
;
若以D、E、P为顶点的三角形与△ABE相似,则△DEP必为直角三角形;
①DE为斜边时,P1在x轴上,此时P1与O重合;
由D(﹣1,0)、E(0,3),得OD=1、OE=3,即tan∠DEO=![]()
![]() =tan∠BAE,即∠DEO=∠BAE
=tan∠BAE,即∠DEO=∠BAE
满足△DEO∽△BAE的条件,因此 O点是符合条件的P1点,坐标为(0,0).
②DE为短直角边时,P2在x轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠DEP2=∠AEB=90°,sin∠DP2E=sin∠BAE=![]()
![]() ;
;
而DE=![]()
![]() =
=![]()
![]() ,则DP2=DE÷sin∠DP2E=
,则DP2=DE÷sin∠DP2E=![]()
![]() ÷
÷![]()
![]() =10,OP2=DP2﹣OD=9
=10,OP2=DP2﹣OD=9
即:P2(9,0);
③DE为长直角边时,点P3在y轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠EDP3=∠AEB=90°,cos∠DEP3=cos∠BAE=![]()
![]() ;
;
则EP3=DE÷cos∠DEP3=![]()
![]() ÷
÷![]()
![]() =
=![]()
![]() ,OP3=EP3﹣OE=
,OP3=EP3﹣OE=![]()
![]() ;
;
综上,得:P1(0,0),P2(9,0),P3(0,﹣![]()
![]() ).
).
(4)解:设直线AB的解析式为y=kx+b.
将A(3,0),B(1,4)代入,得![]()
![]() ,解得
,解得![]()
![]() .
.
∴y=﹣2x+6.
过点E作射线EF∥x轴交AB于点F,当y=3时,得x=![]()
![]() ,∴F(
,∴F(![]()
![]() ,3).
,3).
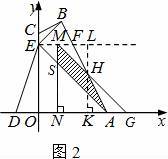
情况一:如图2,当0<t≤![]()
![]() 时,设△AOE平移到△GNM的位置,MG交AB于点H,MN交AE于点S.
时,设△AOE平移到△GNM的位置,MG交AB于点H,MN交AE于点S.
则ON=AG=t,过点H作LK⊥x轴于点K,交EF于点L.
由△AHG∽△FHM,得![]()
![]() ,即
,即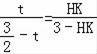
 .
.
解得HK=2t.
∴S阴=S△MNG﹣S△SNA﹣S△HAG=![]()
![]() ×3×3﹣
×3×3﹣![]()
![]() (3﹣t)2﹣
(3﹣t)2﹣![]()
![]() t2t=﹣
t2t=﹣![]()
![]() t2+3t.
t2+3t.
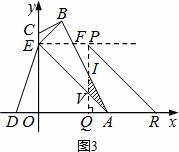
情况二:如图3,当![]()
![]() <t≤3时,设△AOE平移到△PQR的位置,PQ交AB于点I,交AE于点V.
<t≤3时,设△AOE平移到△PQR的位置,PQ交AB于点I,交AE于点V.
由△IQA∽△IPF,得![]()
![]() .即
.即
 ,
,
解得IQ=2(3﹣t).
∵AQ=VQ=3﹣t,
∴S阴=![]()
![]() IVAQ=
IVAQ=![]()
![]() (3﹣t)2=
(3﹣t)2=![]()
![]() t2﹣3t+
t2﹣3t+![]()
![]() .
.
综上所述:s=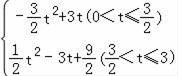
 .
.



【点评】该题考查了二次函数的综合题,涉及到二次函数解析式的确定、切线的判定、相似三角形的判定、图形面积的解法等重点知识,综合性强,难度系数较大.此题的难点在于后两个小题,它们都需要分情况进行讨论,容易出现漏解的情况.在解答动点类的函数问题时,一定不要遗漏对应的自变量取值范围.
(1)操作发现:
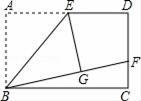
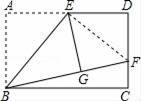
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
(2)问题解决:
保持(1)中的条件不变,若DC=2DF,求![]()
![]() 的值;
的值;
(3)类比探求:
保持(1)中条件不变,若DC=nDF,求![]()
![]() 的值.
的值.

【分析】(1)求简单的线段相等,可证线段所在的三角形全等,即连接EF,证△EGF≌△EDF即可;
(2)可设DF=x,BC=y;进而可用x表示出DC、AB的长,根据折叠的性质知AB=BG,即可得到BG的表达式,由(1)证得GF=DF,那么GF=x,由此可求出BF的表达式,进而可在Rt△BFC中,根据勾股定理求出x、y的比例关系,即可得到![]()
![]() 的值;
的值;
(3)方法同(2).
【解答】解:(1)同意,连接EF,
则根据翻折不变性得,
∠EGF=∠D=90°,EG=AE=ED,EF=EF,
在Rt△EGF和Rt△EDF中,
![]()
![]()
∴Rt△EGF≌Rt△EDF(HL),
∴GF=DF;
(2)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=2DF,
∴CF=x,DC=AB=BG=2x,
∴BF=BG+GF=3x;
在Rt△BCF中,BC2+CF2=BF2,即y2+x2=(3x)2
∴y=2![]()
![]() x,
x,
∴![]()
![]() ;
;
(3)由(1)知,GF=DF,设DF=x,BC=y,则有GF=x,AD=y
∵DC=nDF,
∴BF=BG+GF=(n+1)x
在Rt△BCF中,BC2+CF2=BF2,即y2+[(n﹣1)x]2=[(n+1)x]2
∴y=2x![]()
![]() ,
,
∴![]()
![]() 或
或![]()
![]() .
.

【点评】此题考查了矩形的性质、图形的折叠变换、全等三角形的判定和性质、勾股定理的应用等重要知识,难度适中.
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:![]()
![]() ,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
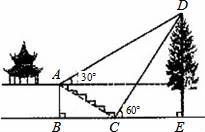

【分析】由于AF⊥AB,则四边形ABEF为矩形,设DE=x,在Rt△CDE中,CE═![]()
![]() =
=![]()
![]() =
=![]()
![]() x,在Rt△ABC中,得到
x,在Rt△ABC中,得到![]()
![]() =
=![]()
![]() ,求出BC,在Rt△AFD中,求出AF,由AF=BC+CE即可求出x的长.
,求出BC,在Rt△AFD中,求出AF,由AF=BC+CE即可求出x的长.
【解答】解:∵AF⊥AB,AB⊥BE,DE⊥BE,
∴四边形ABEF为矩形,
∴AF=BE,EF=AB=2
设DE=x,在Rt△CDE中,CE=![]()
![]() =
=![]()
![]() =
=![]()
![]() x,
x,
在Rt△ABC中,
∵![]()
![]() =
=![]()
![]() ,AB=2,
,AB=2,
∴BC=2![]()
![]() ,
,
在Rt△AFD中,DF=DE﹣EF=x﹣2,
∴AF=![]()
![]() =
=![]()
![]() =
=![]()
![]() (x﹣2),
(x﹣2),
∵AF=BE=BC+CE.
∴![]()
![]() (x﹣2)=2
(x﹣2)=2![]()
![]() +
+![]()
![]() x,
x,
解得x=6.
答:树DE的高度为6米.
【点评】本题考查了解直角三角形的应用﹣﹣仰角、坡度问题、矩形的判定与性质、三角函数;借助仰角构造直角三角形并解直角三角形是解决问题的关键.
已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.
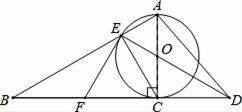

【分析】(1)连接FO,由F为BC的中点,AO=CO,得到OF∥AB,由于AC是⊙O的直径,得出CE⊥AE,根据OF∥AB,得出OF⊥CE,于是得到OF所在直线垂直平分CE,推出FC=FE,OE=OC,再由∠ACB=90°,即可得到结论.
(2)证出△AOE是等边三角形,得到∠EOA=60°,再由直角三角形的性质即可得到结果.
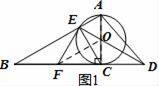
【解答】证明:(1)如图1,连接FO,
∵F为BC的中点,AO=CO,
∴OF∥AB,
∵AC是⊙O的直径,
∴CE⊥AE,
∵OF∥AB,
∴OF⊥CE,
∴OF所在直线垂直平分CE,
∴FC=FE,OE=OC,
∴∠FEC=∠FCE,∠0EC=∠0CE,
∵∠ACB=90°,
即:∠0CE+∠FCE=90°,
∴∠0EC+∠FEC=90°,
即:∠FEO=90°,
∴FE为⊙O的切线;
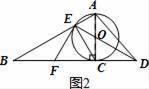
(2)如图2,∵⊙O的半径为3,
∴AO=CO=EO=3,
∵∠EAC=60°,OA=OE,
∴∠EOA=60°,
∴∠COD=∠EOA=60°,
∵在Rt△OCD中,∠COD=60°,OC=3,
∴CD=![]()
![]() ,
,
∵在Rt△ACD中,∠ACD=90°,
CD=![]()
![]() ,AC=6,
,AC=6,
∴AD=![]()
![]() .
.


【点评】本题考查了切线的判定和性质,三角形的中位线的性质,勾股定理,线段垂直平分线的性质,直角三角形的性质,熟练掌握定理是解题的关键.
一种进价为每件40元的T恤,若销售单价为60元,则每周可卖出300件.为提高利润,欲对该T恤进行涨价销售.经过调查发现:每涨价1元,每周要少卖出5件.
(1)请确定该T恤涨价后每周的销售利润y(元)与销售单价x(元)之间的函数关系式,并求销售单价定为多少元时,每周的销售利润最大?
(2)若要使每周的销售利润不低于7680元,请确定销售单价x的取值范围.
【分析】(1)用每件的利润乘以销售量即可得到每周销售利润,即y=(x﹣40)[300﹣5(x﹣60)],再把解析式整理为一般式,然后根据二次函数的性质确定销售单价定为多少元时,每周的销售利润最大.
(2)由函数值求出自变量的两个值,再根据二次不等式的解集即可求得x的取值范围.
【解答】解:(1)根据题意得y=(x﹣40)[300﹣5(x﹣60)]
=﹣5(x2﹣160x+4800)
=﹣5(x﹣80)2+8000,
∵a<0,
∴当x=80时,y的值最大=8000,即销售单价定为80元时,每周的销售利润最大;
(2)当y=7680时,﹣5(x﹣80)2+8000=7680,
整理得:(x﹣80)2=64,
∴x﹣80=±8,
∴x1=88,x2=72,
∴72≤x≤88.
【点评】本题考查了二次函数的应用:利用二次函数解决利润问题,在商品经营活动中,经常会遇到求最大利润,最大销量等问题.解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义,因此在求二次函数的最值时,一定要注意自变量x的取值范围.
本卷还有20题,登录并加入会员即可免费使用哦~

该作品由: 用户孙凌云分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。