2016湖北人教版初中数学中考模拟119604
初中
整体难度：中等
2016-07-21
题号
一
二
三
四
五
评分
一、解答题 (共7题)
添加该题型下试题
1.
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查，调查的运动项目有：篮球、羽毛球、乒乓球、跳绳及其它项目（每位同学仅选一项）．根据调查结果绘制了如下不完整的频数分布表和扇形统计图：
| 运动项目 | 频数（人数） | 频率 |
| 篮球 | 30 | 0.25 |
| 羽毛球 | m | 0.20 |
| 乒乓球 | 36 | n |
| 跳绳 | 18 | 0.15 |
| 其它 | 12 | 0.10 |
请根据以上图表信息解答下列问题：
（1）频数分布表中的m= ，n= ；
（2）在扇形统计图中，“乒乓球”所在的扇形的圆心角的度数为
.
. ；
（3）从选择“篮球”选项的30名学生中，随机抽取3名学生作为代表进行投篮测试，则其中某位学生被选中的概率是 ．
难度：
知识点：圆的有关性质
使用次数：133
【答案】
【分析】（1）根据篮球的人数和所占的百分比求出总人数，再用总人数乘以羽毛球所占的百分比，求出m的值；再用乒乓球的人数除以总人数，求出n的值；
（2）由于已知喜欢乒乓球的百分比，故可用360°×n的值，即可求出对应的扇形圆心角的度数；
用总人数乘以最喜爱篮球的学生人数所占的百分比即可得出答案；
（3）用随机抽取学生人数除以选择“篮球”选项的学生人数，列式计算即可得出答案．
【解答】解：（1）30÷0.25=120（人）
120×0.2=24（人）
36÷120=0.3
故频数分布表中的m=24，n=0.3；
（2）360°×0.3=108°．
故在扇形统计图中，“乒乓球”所在的扇形的圆心角的度数为108°；
（3）3÷30=
．
故其中某位学生被选中的概率是．
故答案为：24，0.3；108°；．
【点评】此题考查了频率分布直方图，用到的知识点是频率=频数÷总数，概率公式，读懂统计表，运用数形结合思想来解决由统计图形式给出的数学实际问题是本题的关键．
2.
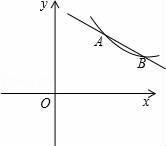
如图，点A（m，m+1），B（m+3，m﹣1）是反比例函数
（x＞0）与一次函数y=ax+b的交点．求：
（1）反比例函数与一次函数的解析式；
（2）根据图象直接写出当反比例函数的函数值大于一次函数的函数值时x的取值范围．
难度：
知识点：反比例函数
使用次数：131
【答案】
【分析】（1）根据反比例函数的特点k=xy为定值，列出方程，求出m的值，便可求出反比例函数的解析式；根据m的值求出A、B两点的坐标，用待定实数法便可求出一次函数的解析式．
（2）根据函数图象可直接解答．
【解答】解：（1）由题意可知，m（m+1）=（m+3）（m﹣1）．
解，得m=3．，B（6，2）；
∴k=4×3=12，
∴
．，B点坐标为（6，2），
∴
，
∴
，
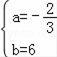
∴y=﹣
x+6．根据图象得x的取值范围：0＜x＜3或x＞6．（7分）
【点评】此题考查的是反比例函数图象上点的坐标特点及用待定系数法求一次函数及反比例函数的解析式，比较简单．
3.
一辆汽车开往距离出发地180千米的目的地，出发后第一小时内按原计划的速度匀速行驶，一小时后以原来的1.5倍匀速行驶，并比原计划提前40分钟到达目的地．求前一小时的行驶速度．
难度：
知识点：分式方程
使用次数：102
【答案】
【分析】设前一小时的速度为x千米/时，则一小时后的速度为1.5x千米/时，等量关系为：加速后用的时间+40分钟+1小时=原计划用的时间．注意加速后行驶的路程为180千米﹣前一小时按原计划行驶的路程．依此列出方程求解即可．
【解答】解：设前一小时的速度为x千米/时，则一小时后的速度为1.5x千米/时，
由题意得：1+
+
=
，
解得x=60．
经检验：x=60是分式方程的解．
答：前一小时的行驶速度为60千米/时．
【点评】本题考查分式方程的应用，分析题意，找到合适的等量关系是解决问题的关键．
4.
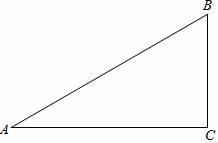
已知：如图，在△ABC中，∠A=30°，∠B=60°．
（1）作∠B的平分线BD，交AC于点D；作AB的中点E（要求：尺规作图，保留作图痕迹，不必写作法和证明）；
（2）连接DE，求证：△ADE≌△BDE．
难度：
知识点：三角形全等的判定
使用次数：200
【答案】
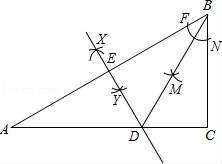
【分析】（1）①以B为圆心，任意长为半径画弧，交AB、BC于F、N，再以F、N为圆心，大于
FN长为半径画弧，两弧交于点M，过B、M画射线，交AC于D，线段BD就是∠B的平分线；
②分别以A、B为圆心，大于AB长为半径画弧，两弧交于X、Y，过X、Y画直线与AB交于点E，点E就是AB的中点；
（2）首先根据角平分线的性质可得∠ABD的度数，进而得到∠ABD=∠A，根据等角对等边可得AD=BD，再加上条件AE=BE，ED=ED，即可利用SSS证明△ADE≌△BDE．
【解答】解：（1）作出∠B的平分线BD；（2分）
作出AB的中点E．证明：
∵∠ABD=×60°=30°，∠A=30°，
∴∠ABD=∠A，（6分）
∴AD=BD，
在△ADE和△BDE中
∴△ADE≌△BDE（SSS）．（8分）
【点评】此题主要考查了复杂作图，以及全等三角形的判定，关键是掌握基本作图的方法和证明三角形全等的判定方法．
5.
先化简，再求值：（x+2y）（x﹣2y）+（x﹣2y）2，其中x=
，y=
．
难度：
知识点：乘法公式
使用次数：149
【答案】
【分析】原式利用平方差公式，完全平方公式化简，去括号合并得到最简结果，把x与y的值代入计算即可求出值．
【解答】解：原式=x2﹣4y2+x2﹣4xy+4y2=2x2﹣4xy，
∵x=
+
，y=﹣
，
∴原式=10﹣4
﹣4=6﹣4．
【点评】此题考查了整式的混合运算﹣化简求值，熟练掌握运算法则是解本题的关键．
本卷还有20题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
25
总体难度：
中等
难度统计
难度系数
数量
占比
中等
11
44.0%
偏难
2
8.0%
容易
12
48.0%
题型统计
大题类型
数量
占比
解答题
7
28.00%
填空题
6
24.0%
选择题
10
40.0%
综合题
2
8.0%
知识点统计
知识点
数量
占比
圆的有关性质
1
4.0%
反比例函数
1
4.0%
分式方程
1
4.0%
三角形全等的判定
1
4.0%
乘法公式
1
4.0%
勾股定理
1
4.0%
解直角三角形与其应用
1
4.0%
二次函数的图象和性质
1
4.0%
等腰三角形
1
4.0%
随机事件与概率
1
4.0%
分式的运算
2
8.0%
弧长和扇形面积
1
4.0%
实际问题与一元二次方程
1
4.0%
特殊的平行四边形
1
4.0%
几何图形
1
4.0%
数据的集中趋势
1
4.0%
一元一次不等式组
1
4.0%
平行线的性质
1
4.0%
有理数的乘方
1
4.0%
有理数
1
4.0%
点和圆、直线和圆的位置关系
1
4.0%
课题学习 选择方案
1
4.0%
相似三角形
1
4.0%
二次函数与一元二次方程
1
4.0%
版权提示
该作品由: 用户萧雨分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。