在平面直角坐标系![]()
![]() 中,图形
中,图形![]() 在坐标轴上的投影长度定义如下:设点
在坐标轴上的投影长度定义如下:设点![]() ,
,![]() 是图形
是图形![]() 上的任意两点.若
上的任意两点.若![]() 的最大值为
的最大值为![]() ,则图形
,则图形![]() 在
在![]() 轴上的投影长度
轴上的投影长度![]() ;若
;若![]() 的最大值为
的最大值为![]() ,则图形
,则图形![]() 在
在![]() 轴上的投影长度
轴上的投影长度![]() .如图,图形
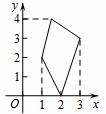
.如图,图形![]() 在
在![]() 轴上的投影长度
轴上的投影长度![]() ;在
;在![]() 轴上的投影长度
轴上的投影长度![]() .
.
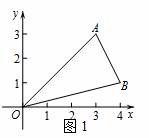
(1)已知点![]() ,
,![]() .如图1所示,若图形
.如图1所示,若图形![]() 为△
为△![]() ,则
,则![]() ,
,![]() .
.
(2)已知点![]() ,点
,点![]() 在直线
在直线![]() 上,若图形
上,若图形![]() 为△
为△![]() .当
.当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(3)若图形![]() 为函数
为函数![]()
![]() 的图象,其中
的图象,其中![]() .当该图形满足
.当该图形满足![]() 时,请直接写出
时,请直接写出![]() 的取值范围.
的取值范围.
(1)4,3.
(2)设点![]() .
.
①当![]() 时,
时,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() (舍去).
(舍去).
②当![]() 时,
时,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍去).
(舍去).
∴![]() .
.
③当![]() 时,
时,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
综上满足条件的![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
(3)![]() .
.
在正方形ABCD中,E为边CD上一点,连接BE.
(1)请你在图1画出△BEM,使得△BEM与△BEC关于直线BE对称;
(2)若边AD上存在一点F,使得AF+CE=EF,请你在图2中探究∠ABF与∠CBE的数量关系并证明;
(3)在(2)的条件下,若点E为边CD的三等分点,且CE<DE,请写出求cos∠FED的思路.(可以不写出计算结果).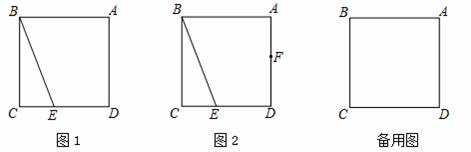
(1)补全图形,如图1所示.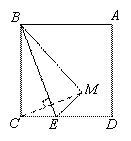
(2)![]() 与
与![]() 的数量关系:
的数量关系:![]() .
.
证明:连接![]() ,
,![]() ,延长
,延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() .
.
∵四边形![]() 为正方形,
为正方形,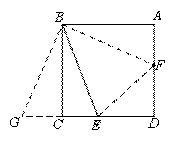
∴![]() ,
,![]() .
.
∴△![]() ≌△
≌△![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() . ∴△
. ∴△![]() ≌△
≌△![]() .
.
∴∠![]() =∠
=∠![]() .
.
∴![]() .
.
(3)求解思路如下:
a.设正方形的边长为![]() ,
,![]() 为
为![]() ,则
,则![]() ,
,![]() ;
;
b.在Rt△![]() 中,由
中,由![]() ,可得
,可得![]()
从而得到![]() 与
与![]() 的关系
的关系![]() ;
;
c.根据cos∠FED![]() ,可求得结果.
,可求得结果.
在平面直角坐标系![]() 中,抛物线C:
中,抛物线C:![]() .
.
(1)当抛物线C经过点![]() 时,
时,![]() 求抛物线的表达式及顶点坐标;
求抛物线的表达式及顶点坐标;
(2)当直线![]() 与直线
与直线![]() 关于抛物线C的对称轴对称时,
关于抛物线C的对称轴对称时,
求![]() 的值;
的值;
(3)若抛物线C:![]()
![]() 与
与![]() 轴的交点的横坐标都在
轴的交点的横坐标都在![]() 和
和![]() 之间(不包括
之间(不包括![]() 和
和![]() ),结合函数的图象,求
),结合函数的图象,求![]() 的取值范围.
的取值范围.
(1)∵抛物线![]() :
:![]() 经过点
经过点![]()
∴![]() ∴
∴![]()
∴![]()
∴![]()
∴抛物线的顶点坐标是![]() .
.
(2)∵直线![]() 与直线
与直线![]() 相交于点
相交于点![]()
∴两直线的对称轴为直线![]() .
.
∵直线![]() 与直线
与直线![]() 关于抛物线
关于抛物线![]() :
:![]()
的对称轴对称
∴![]() ∴
∴![]() .
.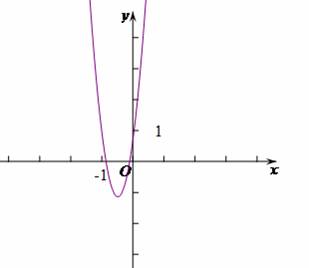
(3)利用函数图像思考,因为抛物线C:![]()
![]() 与
与![]() 轴的交点的横坐标都在
轴的交点的横坐标都在![]() 和
和![]() 之间(不包括
之间(不包括![]() 和
和![]() ),所以当x=-1时,y>0,即m-4+1>0,
),所以当x=-1时,y>0,即m-4+1>0,
得m>3.又因为抛物线与x轴有交点,所以![]() ,得
,得![]()
所以![]() .
.
阅读下面材料:
上课时李老师提出这样一个问题:对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.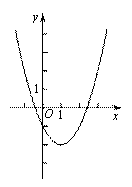
小捷的思路是:原不等式等价于![]() ,设函数
,设函数![]() ,
,![]() ,画出两个函数的图象的示意图,于是原问题转化为函数
,画出两个函数的图象的示意图,于是原问题转化为函数![]() 的图象在
的图象在![]() 的图象上方时
的图象上方时![]() 的取值范围.
的取值范围.
请结合小捷的思路回答:
对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是___________.
的取值范围是___________.
参考小捷思考问题的方法,解决问题:
关于![]() 的方程
的方程![]() 在
在![]() 范围内有两个解,求
范围内有两个解,求![]() 的取值范围.
的取值范围.
![]() 的顶点坐标为(1,-2),函数
的顶点坐标为(1,-2),函数![]() 的图象在
的图象在![]() =a的图象上方,所以
=a的图象上方,所以![]() ;
;
解决问题:
将原方程转化为![]() ·
·
设函数![]() ,
,![]() ,
,
记函数![]() 在
在![]() 内的图象为G,
内的图象为G,
于是原问题转化为![]() 与G有两个
与G有两个
交点时![]() 的取值范围,结合图象可知
的取值范围,结合图象可知![]()
的取值范围是:![]() .
.
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:EF⊥AB;
(2)若∠C=30°,![]() ,求EB的长.
,求EB的长.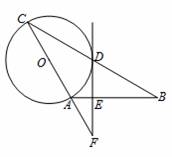
(1)证明:连![]() 接OD,AD,
接OD,AD,
∵AC为⊙O的直径,
∴∠ADC=90°.
又∵AB=AC,
∴CD=DB.又CO=AO,
∴OD∥AB.
∵FD是⊙O的切线,
∴OD⊥DF.∴FE⊥AB.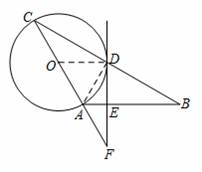
(2)解:∵![]() ,
,
∴![]()
在Rt△![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]()
在Rt△![]() 中,
中,![]() ,
,
∵![]() ,∴
,∴![]() .
.
∵![]() ,
,![]()
∴![]()
![]()
.
∴![]() .
.
本卷还有24题,登录并加入会员即可免费使用哦~

该作品由: 用户笑笑分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。