2016九年级上学期人教版初中数学开学考试114640
初中
整体难度：中等
2015-12-23
题号
一
二
三
四
五
评分
一、解答题 (共31题)
添加该题型下试题
1.
某中学开展“感恩父母”演讲比赛活动，八（1）、八（2）班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如下图所示。
（1）根据下图，分别求出两班复赛的平均成绩和方差；
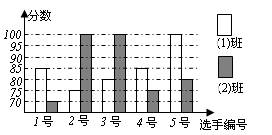
（2）根据（1）的计算结果，哪个班级的复赛成绩较好？为什么？
难度：
知识点：统计调查
使用次数：200
【答案】
1）85，70；85，160；（2）八（1）.
【解析】
试题分析：（1）从直方图中得到各个选手的得分，由平均数和方差的公式计算；
（2）由方差的意义分析．
试题解析：（1）八（1）班的选手的得分分别为85，75，80，85，100，
∴八（1）班的平均数=（85+75+80+85+100）÷5=85，
八（1）班的方差S12=[（85-85）2+（75-85）2+（80-85）2+（85-85）2+（100-85）2]÷5=70；
八（2）班的选手的得分分别为70，100，100，75，80，
八（2）班平均数=（70+100+100+75+80）÷5=85，
八（2）班的方差S22=[（70-85）2+（100-85）2+（100-85）2+（75-85）2+（80-85）2]÷5=160；
（2）平均数一样的情况下，八（1）班方差小，成绩比较稳定，所以成绩比较好．
【难度】一般
2.
五一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加
，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分）之间的关系如图所示．
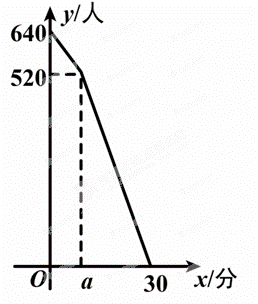
（1）求a的值．
（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问：检票一开始至少需要同时开放几个检票口？
难度：
知识点：课题学习 选择方案
使用次数：104
【答案】
（1）10 （2）260 （3）5
【解析】
解：（1）由图象知，640＋16a－2×14a＝520，∴a＝10．
（2）设当10≤x≤30时，y与x之间的函数关系式为y＝kx＋b（k≠0），由题意得
解得
∴y＝－26x＋780．
当x＝20时，y＝260，即检票到第20分钟时，候车室排队等候检票的旅客有260人．
（3）设需同时开放n个检票口，则由题意知
14n×15≥640＋16×15，
解得
，
∵n为整数，
∴n＝5．
答：至少需要同时开放5个检票口．
【难度】较难
3.
如图，直线l上有一点P1（2，1），将点P1先向右平移1个单位，再向上平移2个单位得到像点P2，点P2恰好在直线l上．
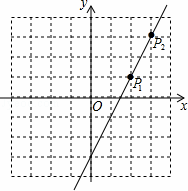
（1）写出点P2的坐标；
（2）求直线l所表示的一次函数的表达式；
（3）若将点P2先向右平移3个单位，再向上平移6个单位得到像点P3．请判断点P3是否在直线l上，并说明理由．
难度：
知识点：课题学习 选择方案
使用次数：141
【答案】
（1）P2（3，3）；（2）y=2x﹣3；（3）在．
【解析】
试题分析：本题考查了待定系数法求一次函数解析式，一次函数图象上点的坐标特征以及一次函数图象的几何变换．在平面直角坐标系中，图形的平移与图形上某点的平移相同．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．（1）根据平移规律来求点P2的坐标；
（2）设直线l所表示的一次函数的表达式为y=kx+b（k≠0），把点P1（2，1），P2（3，3）代入直线方程，利用方程组来求系数的值；（3）把点（6，9）代入（2）中的函数解析式进行验证即可．
试题解析：（1）P2（3，3）．
（2）设直线l所表示的一次函数的表达式为y=kx+b（k≠0），
∵点P1（2，1），P2（3，3）在直线l上， ∴
， 解得
．
∴直线l所表示的一次函数的表达式为y=2x﹣3．
（3）点P3在直线l上．由题意知点P3的坐标为（6，9）， ∵2×6﹣3=9，
∴点P3在直线l上．
【难度】一般
4.
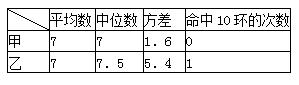
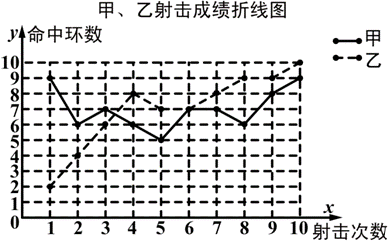
为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶10次，为了比较两人的成绩，制作了统计表和统计图：
甲、乙射击成绩统计表
| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 0 | ||
| 乙 | 1 |
（1）请补全上述图表（直接在表中填空和补全折线图）；
（2）如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由；
（3）如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？
难度：
知识点：数据的波动程度
使用次数：164
【答案】
（1）甲、乙射击成绩统计表
（2）甲
（3）希望乙胜出，规则为命中9环与10环的总数大的胜出．因为乙命中9环与10环的总数为3次，而甲只命中2次．
【解析】
（1）根据折线统计图得乙的射击成绩为2，4，6，7，7，8，8，9，9，10，则平均数为
，中位数为7．5，方差为
×[（2－7）2＋（4－7）2＋（6－7）2＋（8－7）2＋（7－7）2＋（7－7）2＋（8－7）2＋（9－7）2＋（9－7）2＋（10－7）2]＝5．4；
由表知甲的射击成绩的平均数为7，则甲第8次射击成绩为70－（9＋6＋7＋6＋5＋7＋7＋8＋9）＝6（环），故10次射击成绩为5，6，6，6，7，7，7，8，9，9，中位数为7，方差为×[（5－7）2＋（6－7）2＋（6－7）2＋（6－7）2＋（7－7）2＋（7－7）2＋（7－7）2＋（8－7）2＋（9－7）2＋（9－7）2]＝1．6，补全图表如下：
甲、乙射击成绩统计表
（2）因为两人射击成绩的平均数相同，但甲的方差小于乙的方差，故甲胜出．
（3）希望乙胜出，规则为命中9环与10环的总数大的胜出．因为乙命中9环与10环的总数为3次，而甲只命中2次．
【难度】困难
5.
A、B两个火车站相距360km．一列快车与一列普通列车分别从A，B两站同时出发相向而行，快车的速度比普通列车的速度快54km/h，当快车到达B站时，
普通列车距离A站还有135km．求快车和普通列车的速度各是多少？
难度：
知识点：分式方程
使用次数：63
【答案】
普通列车的速度为90km/h，快车的速度为144km/h．
【解析】
试题分析：首先设普通列车的速度为xkm/h，则快车的速度为（x+54）km/h，根据题意列出分式方程，然后进行求解，最后需要进行验根．
试题解析：设普通列车的速度为xkm/h，则快车的速度为（x+54）km/h
由题意，得：
解得：x=90
经检验得：x=90是这个分式方程的解．x+54=144．
答：普通列车的速度为90km/h，快车的速度为144km/h．
【难度】一般
本卷还有26题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
31
总体难度：
中等
难度统计
难度系数
数量
占比
中等
28
90.32%
偏难
1
3.22%
容易
2
6.45%
题型统计
大题类型
数量
占比
解答题
31
100.0%
知识点统计
知识点
数量
占比
统计调查
4
12.90%
课题学习 选择方案
10
32.25%
数据的波动程度
2
6.45%
分式方程
3
9.67%
数据的集中趋势
2
6.45%
二次根式的加减
1
3.22%
反比例函数
4
12.90%
平行线的性质
1
3.22%
用列举法求概率
1
3.22%
解一元二次方程
1
3.22%
实际问题与一元二次方程
1
3.22%
一次函数
1
3.22%
版权提示
该作品由: 用户赵吕品分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。