函数![]() 中,自变量x的取值范围是
中,自变量x的取值范围是
A.x>﹣1 B.x<﹣1 C.x≠﹣1 ![]() D.x≠0
D.x≠0
C
【解析】
试题分析:求函数自变量的取值范围,就是求函数解析式有意义的条件,根据分式分母不为0的条件,要使![]() 在实数范围内有意义,必须
在实数范围内有意义,必须![]() 。故选C。
。故选C。
小文、小亮从学校出发到青少年宫参加书法比赛,小文步行一段时间后,小亮骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小文出发时间t(分)之间的函数关系如图所示.下列说法:①小亮先到达青少年宫;②小亮的速度是小文速度的2.5倍;③a=24;④b=480.其中正确的是
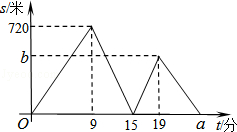
A.①②③ B.①②④ C.①③④ D.①②③④
B
【解析】
试题分析:由图象得出小文步行720米,需要9分钟,所以小文的运动速度为:720÷9=80(m/t)。
当第15钟时,小亮运动15﹣9=6(分钟),运动距离为:15×80=1200(m),
∴小亮的运动速度为:1200÷6=200(m/t)。
∴200÷80=2.5,故②小亮的速度是小文速度的2.5倍正确。
当第19分钟以后两人之间距离越来远近,说明小亮已经到达终点,故①小亮先到达青少年宫正确。
此时小亮运动19﹣9=10(分钟),运动总距离为:10×200=2000(m)。
∴小文运动时间为:2000÷80=25(分钟),故a的值为25,故③a=24错误。
∵小文19分钟运动距离为:19×80=1520(m),
∴b=2000﹣1520=480,故④b=480正确。
综上所述,正确的有:①②④。故选B。
如图,在直角梯形ABCD中,AB=2,BC=4,AD=6,M是CD的中点,点P在直角梯形的边上沿A→B→C→M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示是
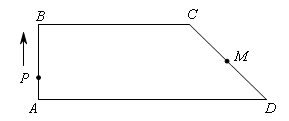
A.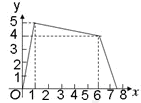 B.
B.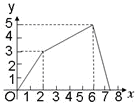 C.
C.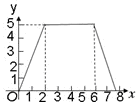 D.
D.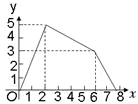
D
【解析】
试题分析:应用特殊元素法和排他法进行分析:
当点P运动到点B时,如图1,
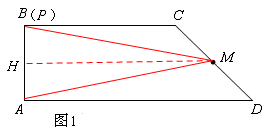
作AB边上的高MH,
∵AB=2,BC=4,AD=6,M是CD的中点,
∴MH是梯形的中位线。∴MH=![]() 。
。
∴△APM的面积=![]() 。
。
∴当x=2时,y=5。从而可排除A,B选项。
当点P运动到点C时,如图2,
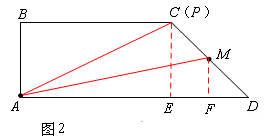
分别作△ACD和△AMD的AD边H的高CE和MF,
∵AB=2,BC=4,AD=6,M是CD的中点,
∴MF是△CDE的中位线。∴MF=![]() 。
。
∴△APM的面积![]() 。
。
∴当x=6时,y=3。从而可排除C选项。
故选D。
若正比例函数y=mx(m≠0),y随x的增大而减小,则它和二次函数y=mx2+m的图象大致是【 】
A.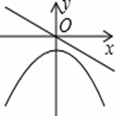 B.
B.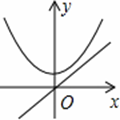 C.
C.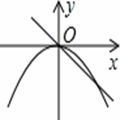 D.
D.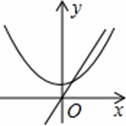
A。
【解析】∵正比例函数y=mx(m≠0),y随x的增大而减小,
∴该正比例函数图象经过第一、三象限,且m<0。
∴二次函数y=mx2+m的图象开口方向向下,且与y轴交于负半轴.
综上所述,符合题意的只有A选项。故选A。
已知一次函数y=x﹣2,当函数值y>0时,自变量x的取值范围在数轴上表示正确的是【 】
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
B。
【解析】∵一次函数y=x﹣2,
∴函数值y>0时,x﹣2>0,解得,x>2。
不等式的解集在数轴上表示的方法:>,≥向右画;<,≤向左画,在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示![]() 。因此不等式x>2在数轴上表示正确的是B。故选B。
。因此不等式x>2在数轴上表示正确的是B。故选B。
本卷还有45题,登录并加入会员即可免费使用哦~

该作品由: 用户孙永亮分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。