2013河北七年级下学期人教版初中数学期末考试68054
初中
整体难度：中等
2013-09-07
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
64的立方根是（ ）
|
| A． | 8 | B． | ±8 | C． | 4 | D． | ±4 |
难度：
知识点：立方根
使用次数：133
【答案】
C考点：
立方根．
专题：
计算题．
分析：
如果一个数x的立方等于a，那么x是a的立方根，根据此定义求解即可．
解答：
解：∵4的立方等于64，
∴64的立方根等于4．
故选C．
点评：
此题主要考查了求一个数的立方根，解题时应先找出所要求的这个数是哪一个数的立方．由开立方和立方是互逆运算，用立方的方法求这个数的立方根．注意一个数的立方根与原数的性质符号相同．
2.
如图所示的网格中各有不同的图案，不能通过平移得到的是（ ）
|
| A． |
| B． |
| C． |
| D． |
|
难度：
知识点：平移
使用次数：121
【答案】
考点：
生活中的平移现象．
分析：
根据平移的定义：在平面内，把一个图形整体沿某一的方向移动，这种图形的平行移动，叫做平移变换，结合各选项所给的图形即可作出判断．
解答：
解：A、可以通过平移得到，不符合题意；
B、可以通过平移得到，不符合题意；
C、不可以通过平移得到，符合题意；
D、可以通过平移得到，不符合题意．
故选：C．
点评：
本题考查平移的性质，属于基础题，要掌握图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转．
3.
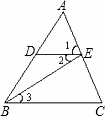
如图，下列推理及所注明的理由都正确的是（ ）
|
| A． | 因为DE∥BC，所以∠1=∠C（同位角相等，两直线平行） |
|
| B． | 因为∠2=∠3，所以DE∥BC（两直线平行，内错角相等） |
|
| C． | 因为DE∥BC，所以∠2=∠3（两直线平行，内错角相等） |
|
| D． | 因为∠1=∠C，所以DE∥BC（两直线平行，同位角相等） |
难度：
知识点：平行线的性质
使用次数：186
【答案】
考点：
平行线的判定与性质．
分析：
A的理由应是两直线平行，同位角相等；
B的理由应是内错角相等，两直线平行；
D的理由应是同位角相等，两直线平行；
所以正确的是C．
解答：
解：A、因为DE∥BC，所以∠1=∠C（两直线平行，同位角相等）；
B、因为∠2=∠3，所以DE∥BC（内错角相等，两直线平行）；
C、因为DE∥BC，所以∠2=∠3（两直线平行，内错角相等）；
D、因为∠1=∠C，所以DE∥BC（同位角相等，两直线平行）．
故选C．
点评：
正确区分平行线的性质和判定是解决此类问题的关键．
4.
将100个数据分成8个组，如下表：则第六组的频数为（ ）
| 组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频数 | 11 | 14 | 12 | 13 | 13 | x | 12 | 10 |
|
| A． | 12 | B． | 13 | C． | 14 | D． | 15 |
难度：
知识点：统计调查
使用次数：104
【答案】
考点：
频数与频率．
专题：
图表型．
分析：
根据各组频数的和是100，即可求得x的值．
解答：
解：根据表格，得
第六组的频数x=100﹣（11+14+12+13+13+12+10）=15．
故选D．
点评：
本题是对频率、频数灵活运用的综合考查．
各小组频数之和等于数据总和；各小组频率之和等于1．
5.
不等式组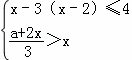
无解，则a的取值范围是（ ）
|
| A． | a＜1 | B． | a≤1 | C． | a＞1 | D． | a≥1 |
难度：
知识点：一元一次不等式组
使用次数：160
【答案】
考点：
解一元一次不等式组．
分析：
先求不等式组的解集，再逆向思维，要不等式组无解，x的取值正好在不等式组的解集之外，从而求出a的取值范围．
解答：
解：原不等式组可化为
，即
，
故要使不等式组无解，则a≤1．
故选B．
点评：
解答此题的关键是熟知不等式组的解集的求法应遵循：“同大取较大，同小取较小，小大大小中间找，大大小小解不了”的原则．
本卷还有16题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
21
总体难度：
中等
难度统计
难度系数
数量
占比
基础
1
4.76%
中等
12
57.14%
容易
8
38.09%
题型统计
大题类型
数量
占比
选择题
10
47.61%
填空题
7
33.33%
解答题
4
19.04%
知识点统计
知识点
数量
占比
立方根
1
4.76%
平移
1
4.76%
平行线的性质
3
14.28%
统计调查
3
14.28%
一元一次不等式组
2
9.52%
不等式
1
4.76%
消元 解二元一次方程组
1
4.76%
坐标方法的简单应用
2
9.52%
有理数的加减法
1
4.76%
一元一次不等式
1
4.76%
二元一次方程组
1
4.76%
相交线
1
4.76%
平面直角坐标系
1
4.76%
与三角形有关的角
1
4.76%
实际问题与二元一次方程组
1
4.76%
版权提示
该作品由: 用户毛小毛分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。