2013湖北七年级下学期人教版初中数学期末考试67625
初中
整体难度：中等
2013-09-01
题号
一
二
三
四
五
评分
一、填空题 (共10题)
添加该题型下试题
1.
的平方根是
难度：
知识点：平方根
使用次数：135
【答案】
±
．
| 考点： | 平方根． |
| 分析： | 先把带分数化为假分数，再根据平方根的定义解答． |
| 解答： | 解：∵2 ∴2 故答案为：± |
| 点评： | 本题考查了平方根的定义，是基础题，要注意把带分数化为假分数． |
=
=（±
）2.
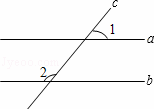
如图，直线a、b被第三条直线c所截，如果a∥b，∠1=50°，那么∠2= °
．
难度：
知识点：平行线的性质
使用次数：138
【答案】
考点：
平行线的性质．
分析：
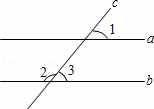
由a∥b，∠1=50°，根据两直线平行，同位角相等，即可求得∠3的度数，然后邻补角的定义，即可求得∠2的度数．
解答：
解：a∥b，∠1=50°，
∴∠3=∠1=50°，
∵∠2+∠3=180°，
∴∠2=130°．
故答案为：130°．
点评：
此题考查了平行线的性质与邻补角的定义．此题难度不大，解题的关键是注意掌握两直线平行，同位角相等定理的应用．
3.
如果用（7，8）表示七年级八班，那么八年级七班可表示成 （8，7） ，（9，4）表示的含义是
难度：
知识点：坐标方法的简单应用
使用次数：196
【答案】
九年级四班 ．
| 考点： | 坐标确定位置． |
| 分析： | 由于用（7，8）表示七年级八班，根据这个表示方法即可得到八年级七班怎么表示，也可以知道（9，4）表示的含义． |
| 解答： | 解：∵用（7，8）表示七年级八班， ∴八年级七班表示为（8，7）， （9，4）表示的含义是九年级四班． |
| 点评： | 此题考查利用点的坐标解决实际问题的能力和阅读理解能力，解决这类问题必须是正确理解题意，根据题意解决问题． |
4.
已知二元一次方程4x+3y=9，若用含x的代数式表示y，则有y=
难度：
知识点：消元 解二元一次方程组
使用次数：151
【答案】
．
| 考点： | 解二元一次方程． |
| 分析： | 先移项，再把y的系数化为1即可． |
| 解答： | 解：移项得，3y=9﹣4x， 把y的系数化为1得，y=3﹣ 故答案为：3﹣ |
| 点评： | 本题考查的是解二元一次方程，熟知解二元一次方程的基本步骤是解答此题的关键． |
x．
5.
若
+
有意义，则
=
难度：
知识点：二次根式
使用次数：53
【答案】
1 ．
| 考点： | 二次根式有意义的条件． |
| 分析： | 根据二次根式的被开方数是非负数得到x=0，由此可以求得 |
| 解答： | 解：由题意，得
解得x=0， 则 故答案是：1． |
| 点评： | 考查了二次根式的意义和性质．概念：式子 |
=1．
（a≥0）叫二次根式．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．本卷还有22题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
27
总体难度：
中等
难度统计
难度系数
数量
占比
容易
9
33.33%
中等
18
66.66%
题型统计
大题类型
数量
占比
填空题
10
37.03%
选择题
8
29.62%
计算题
2
7.40%
解答题
7
25.92%
知识点统计
知识点
数量
占比
平方根
1
3.70%
平行线的性质
5
18.51%
坐标方法的简单应用
3
11.11%
消元 解二元一次方程组
4
14.81%
二次根式
1
3.70%
平面直角坐标系
1
3.70%
二元一次方程组
1
3.70%
一元一次不等式组
3
11.11%
统计调查
2
7.40%
平行线及其判定
1
3.70%
一元一次不等式
1
3.70%
实数
1
3.70%
实际问题与二元一次方程组
2
7.40%
实际问题与一元一次方程
1
3.70%
版权提示
该作品由: 用户竹欣分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。