若 ,则 m 的值为( )
A . 8 B . 6 C . 5 D . 2
B
【分析】根据同底数幂的乘法运算计算 ,即可求解.
【详解】 ,
,
故选: B .
【点睛】本题考查了同底数幂的乘法运算,即 ( m 、 n 为正整数),熟练掌握运算法则是解题的关键.
若 a , b 互为相反数, c 的倒数是 4 ,则 的值为( )
A . B .
C .
D . 16
C
【分析】根据 a , b 互为相反数,可得 , c 的倒数是 4 ,可得
, 代入即可求解.
【详解】 ∵ a , b 互为相反数,
∴ ,
∵ c 的倒数是 4 ,
∴ ,
∴
,
故选: C
【点睛】本题考查了代数式的求值问题,利用已知求得 ,
是 解题的关键.
若 ,则下列不等式中正确的是( )
A . B .
C .
D .
D
【分析】根据不等式的性质:不等式的两边都加(或减)同一个数,不等号的方向不变,不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;不等式的两边都乘以(或除以)同一个负数,不等号的方向改变,可得答案.
【详解】解: A 、 ∵ m > n , ∴ ,故本选项不合题意;
B 、 ∵ m > n , ∴ ,故本选项不合题意;
C 、 ∵ m > n , ∴ ,故本选项不合题意;
D 、 ∵ m > n , ∴ ,故本选项符合题意;
故选: D .
【点睛】本题考查了不等式的性质,不等式的基本性质是解不等式的主要依据,必须熟练地掌握.要认真弄清不等式的基本性质与等式的基本性质的异同,特别是在不等式两边同乘以(或除以)同一个数时,不仅要考虑这个数不等于 0 ,而且必须先确定这个数是正数还是负数,如果是负数,不等号的方向必须改变.
几个大小相同,且棱长为 1 的小正方体所搭成几何体的俯视图如图所示,图中小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图的面积为( )
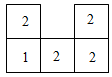
A . 3 B . 4 C . 6 D . 9
B
【分析】根据该几何体的俯视图以及该位置小正方体的个数,可以画出左视图,从而求出左视图的面积;
【详解】由俯视图以及该位置小正方体的个数,左视图共有两列,第一列两个小正方体,第二列两个小正方体,可以画出左视图如图,
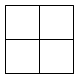
所以这个几何体的左视图的面积为 4
故选: B
【点睛】本题考查了物体的三视图,解题的关键是根据俯视图,以及该位置小正方体的个数,正确作出左视图.
2022 年 2 月 20 日北京冬奥会大幕落下,中国队在冰上、雪上项目中,共斩获 9 金 4 银 2 铜,创造中国队冬奥会历史最好成绩某校为普及冬奥知识,开展了校内冬奥知识竞赛活动,并评出一等奖 3 人.现欲从小明等 3 名一等奖获得者中任选 2 名参加全市冬奥知识竞赛,则小明被选到的概率为( )
A . B .
C .
D .
D
【分析】根据题意,列出树状图,即可得出答案.
【详解】记小明为 ,其他 2 名一等奖为
,
列树状图如下:
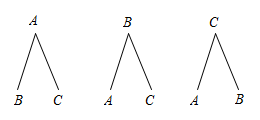
故有 6 种等可能性结果,其中小明被选中得有 4 种,故明被选到的概率为 .
故选: D .
【点睛】此题考查了列表法或树状图法 : 通过列表法或树状图法展示所有等可能的结果求出 n ,再从中选出符合事件 A 或 B 的结果数目 m ,然后根据概率公式求出事件 A 或 B 的概率.
本卷还有20题,登录并加入会员即可免费使用哦~

该作品由: 用户and one分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。