将一个直角三角板和一把直尺如图放置,如果 ,则
的度数是( )
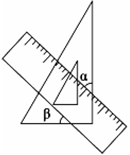
A . 43° B . 47° C . 30° D . 45°
B
【分析】如图:延长 BC 交刻度尺的一边于 D 点,再利用平行线的性质、对顶角的性质,将已知角与所求角转化到 Rt△ CDE 中,最后利用三角形内角和定理求解即可.
【详解】解:如图,延长 BC 交刻度尺的一边于 D 点,
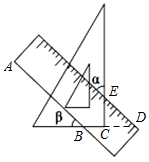
∵ AB DE ,
∴∠ β = ∠ EDC ,
又 ∵∠ CED = ∠ α = 43° , ∠ ECD = 90° ,
∴∠ β = ∠ EDC = 90° ﹣ ∠ CED = 90° ﹣ 46° = 47° .
故选: B .
【点睛】本题主要考查了平行线的性质、三角形内角和定理等知识点,根据题意作出辅助线,构造出平行线是解答本题的关键.
如图,已知四边形纸片 ABCD 中, ∠ B = 70° , ∠ C = 80° ,将纸片折叠,使 C 、 D 落在 AB 上的 C ′ 、 D ′ 处,折痕为 MN ,则 ∠ MNC ′ 的度数为( )
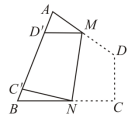
A . 70° B . 75° C . 80° D . 85°
D
【分析】根据折叠的性质可得 ,根据三角形的外角的性质可得
,进而可得
,根据折叠的性质即可求解.
【详解】由折叠可知 ,
∴ ,
∴ ,
∴ .
故选 D .
【点睛】本题考查了折叠的性质,三角形外角的性质,掌握三角形的外角的性质求得 是解题的关键.
2022 年 2 月 4 日,北京冬奥会开幕式为世界奉献了一场精彩,简约,唯美,浪漫的中国文化盛宴,其中主火炬台的雪花状创意令人惊叹如图是一个正六边形雪花状饰品,则它的每一个内角是( )
A . B .
C .
D .
C
【分析】根据多边形的内角和公式:多边形的内角和 = 和正多边形的性质即可求解.
【详解】解: ∵ 正六边形的内角和为: ,
又 ∵ 正六边形的 6 个内角都相等,
∴ 它的每一个内角 = .
故选 C .
【点睛】本题考查多边形的内角和公式和正多边形的性质.掌握多边形的内角和 = 与正多边形的每一个内角都相等是解题关键.
如图所示在 中,
边上的高线画法正确的是( )
A . 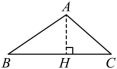 B .
B . 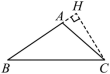 C .
C . 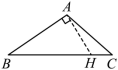 D .
D . 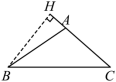
B
【分析】经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,由此解答即可.
【详解】解: A 选项,画的是 中 BC 上的高,故不符合题意;
B 选项,画的是 中 AB 上的高,故符合题意;
C 选项,画的不是 的高线,故不符合题意;
D 选项,画的是 中 AC 上的高,故不符合题意;
故选: B .
【点睛】本题主要考查了三角形高线的作法,正确把握相关定义是解题关键.
下列各组数,可以作为三角形的三边长的是( )
A . 2 , 3 , 5 B . 7 , 10 , 25 C . 8 , 12 , 20 D . 5 , 13 , 15
D
【分析】根据两边和大于第三边,两边差小于第三边进行判断即可.
【详解】解: A 、 ,故不能构成三角形,不符合题意;
B 、 ,故不能构成三角形,不符合题意;
C 、 ,故不能构成三角形,不符合题意;
D 、 ,可以构成三角形,符合题意;
故选: D .
【点睛】本题考查了三角形的三边关系,熟知 “ 两边和大于第三边,两边差小于第三边 ” 是解本题的关键.
本卷还有30题,登录并加入会员即可免费使用哦~

该作品由: 用户卢宣渝分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。