在下列正多边形中,其内角是中心角 2 倍的是( )
A .正四边形 B .正五边形 C .正六边形 D .正七边形
C
【分析】设多边形的边数是 n .每个内角是 ,中心角是
,根据内角是中心角 2 倍,建立方程解方程即可求解.
【详解】解:设多边形的边数是 n .
则每个内角是 ,中心角是
.
根据题意得: = 2×
解得: n = 6 .
故选: C .
【点睛】本题考查了正多边形的性质,多边形内角和公式,根据题意建立方程是解题的关键.
如图所示, AB 是 ⊙ O 的直径, AD = DE , AE 与 BD 交于点 C ,则图中与 ∠ BCE 相等的角除对顶角外还有( )
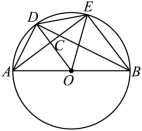
A . 2 个 B . 3 个 C . 4 个 D . 5 个
C
【分析】首先与 ∠ BCE 相等的角有对顶角 ∠ DCA .由于 AB 是 ⊙ O 的直径,可得 ∠ ADB =90° ;已知 AD = DE ,证明 △ OAD ≌△ OED ,因此 ∠ DAB =∠ ADO =∠ ODE =∠ DEO ;由 AD = DE 得出 ,得出 ∠ ABD =∠ DBE ,得出 ∠ DAB =∠ BCE ,因此与 ∠ BCE 相等的角有 5 个: ∠ DCA 、 ∠ OAD 、 ∠ ODA 、 ∠ ODE 、 ∠ OED .
【详解】解: ∵ 在 △ ADO 和 △ DOE 中
,
∴△ OAD ≌△ ODE ( SSS ),
∴∠ DAB =∠ EDO , ∠ ADO =∠ DEO ,
∵ AO = DO ,
∴∠ DAB =∠ ADO ,
∴∠ DAB =∠ ADO =∠ ODE =∠ DEO ;
∵ AB 是 ⊙ O 的直径,
∴∠ ADB =90° , ∠ AEB =90° ,
∵ AD = DE ,
∴ ,
∴∠ ABD =∠ DBE ,
∴∠ DAB =90°-∠ ABD , ∠ BCE =90°-∠ DBE ,
∴∠ DAB =∠ BCE ,
∴∠ DCA =∠ DAB =∠ ADO =∠ ODE =∠ DEO ,
则与 ∠ ECB 相等的角有 5 个.
图中与 ∠ BCE 相等的角除对顶角外还有 4 个
故选 C .
【点睛】此题主要考查圆周角定理,以及等腰三角形的性质,关键是掌握同弧所对的圆周角相等.
用反证法证明: “ 在一个三角形中,至少有一个内角小于或等于 60°” 时,第一步先假设( )
A .三角形中有一个内角小于 60° B .三角形中有一个内角大于 60°
C .三角形中每个内角都大于 60° D .三角形中没有一个内角小于 60°
C
【分析】根据反证法的步骤中,第一步是假设结论不成立,反面成立解答.
【详解】解:用反证法证明: “ 在一个三角形中,至少有一个内角小于或等于 60°” 时,
第一步先假设三角形中每个内角都大于 60° .
故选: C
【点睛】本题考查的是反证法,解此题关键要懂得反证法的意义及步骤.反证法的步骤是:( 1 )假设结论不成立;( 2 )从假设出发推出矛盾;( 3 )假设不成立,则结论成立.
用反证法证明命题 “ 四边形中至少有一个角是钝角或直角 ” 时,应 ( )
A .假设四边形 ABCD 中没有一个角是钝角或直角
B .假设四边形 ABCD 中至少有一个角是钝角或直角
C .假设四边形 ABCD 中最多有一个角是钝角或直角
D .假设四边形 ABCD 中没有一个角是锐角
A
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立.
【详解】解:用反证法证明命题 “ 四边形中至少有一个角是钝角或直角 ” 时,应假设四边形 ABCD 中没有一个角是钝角或直角.
故选: A
【点睛】此题考查了反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
如图,圆锥的高 为 4 ,母线
长为 5 ,则该圆锥展开图的弧长等于( )
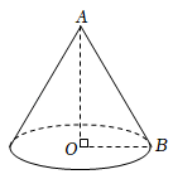
A . B .
C .
D .
C
【分析】利用勾股定理易得圆锥的底面半径,利用底面周长即为扇形的弧长计算即可.
【详解】解: 圆锥的高
为 4 ,母线
长为 5 ,
由勾股定理得:圆锥的底面半径为:
,
展开扇形的弧长为:
,故 C 正确.
故选: C .
【点睛】本题主要考查圆锥侧面积公式的运用,注意运用圆锥的高,母线长,底面半径组成直角三角形这个知识点.
本卷还有30题,登录并加入会员即可免费使用哦~

该作品由: 用户叶枕寒分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。