2021-2022学年初中八年级第二十二单元数学练习题含解析
初中
整体难度：中等
2022-06-05
题号
一
二
三
四
五
评分
一、选择题 (共20题)
添加该题型下试题
1.
二次函数 y =− x 2 +4 x +7 的顶点坐标和对称轴分别是（ ）
A ． ， x ＝ 2 B ．
， x ＝ 2 C ．
， x ＝－ 2 D ．
， x ＝ 2
难度：
知识点：函数
使用次数：206
【答案】
A
【解析】
【分析】
将题目中函数解析式化为顶点式，从而可以得到该函数的顶点坐标和对称轴，本题得以解决．
【详解】
解： ∵ y =- x 2 +4 x +7
=- （ x -2 ） 2 +11 ，
∴ 该函数的顶点坐标是（ 2 ， 11 ），对称轴是直线 x =2 ．
故选： A ．
【点睛】
本题考查二次函数的性质，解答本题的关键是明确二次函数的性质，利用二次函数的顶点式解答．
2.
二次函数 与 x 轴的两个交点的横坐标分别为 m 和 n ，且
，下列结论正确的是（ ）
A ． B ．
C ．
D ．
难度：
知识点：二次函数的图象和性质
使用次数：250
【答案】
C
【解析】
【分析】
根据题意画出二次函数 及
的图象，观察图象即可得出结论。
【详解】
解：由题意得，二次函数 与 x 轴的交点为 a 、 b ，将其图象向上平移三个单位长度即可得到二次函数
的图象，如图所示，
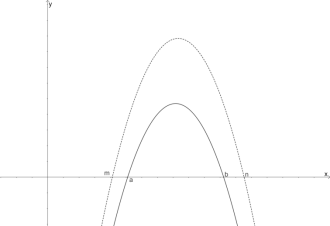
可知： ，
故选： C ．
【点睛】
本题考查了抛物线与 x 轴的交点以及二次函数的图象，依照题意画出图象，利用数形结合解决问题是解题的关键．
3.
小明研究二次函数 （ m 为常数）性质时，得出如下结论： ① 这个函数图象的顶点始终在直线 y ＝ x － 1 上； ② 存在两个 m 的值，使得函数图象的顶点与 x 轴的两个交点构成等腰直角三角形； ③ 点
与点
在函数图象上，若
，
，则
； ④ 当
时， y 随 x 的增大而减小，则 m 的取值范围为
．其中错误结论的序号是（ ）
A ． ① B ． ② C ． ③ D ． ④
难度：
知识点：二次函数的图象和性质
使用次数：229
【答案】
B
【解析】
【分析】
根据函数解析式，结合函数图象的顶点坐标、对称轴以及增减性依次对 4 个结论作出判断即可．
【详解】
解：二次函数 （ m 为常数）
∴ 顶点坐标为（ m ， m -1 ）
把 x = m 代入 y ＝ x － 1 ，得： y = m -1 ，
∴ 这个函数图象的顶点始终在直线 y = x -1 上
故结论 ① 正确；
② 假设存在一个 m 的值，使得函数图象的顶点与 x 轴的两个交点构成等腰直角三角形
令 y =0 ，得（ x - m ） 2 + m -1=0 ，其中 m ≤1
解得： ，
∵ 顶点坐标为（ m ， m -1 ），且顶点与 x 轴的两个交点构成等腰直角三角形
∴| m -1|=| m - （ m - ） |
解得： m =0 或 1 ，
当 m =1 时，二次函数 y = （ x -1 ） 2 ，此时顶点为（ 1 ， 0 ），与 x 轴的交点也为（ 1 ， 0 ），不构成三角形，舍去；
∴ 存在 m =0 ，使得函数图象的顶点与 x 轴的两个交点构成等腰直角三角形
故结论 ② 错误；
③∵ x 1 + x 2 ＞ 2 m
∴ ＞ m
∵ 二次函数 y = （ x - m ） 2 + m -1 （ m 为常数）的对称轴为直线 x = m
∴ 点 A 离对称轴的距离小于点 B 离对称轴的距离
∵ x 1 ＜ x 2 ，且 a =1 > 0
∴ y 1 < y 2
故结论 ③ 正确；
④ 当 -1 ＜ x ＜ 3 时， y 随 x 的增大而减小，且 a =1 > 0
∴ m 的取值范围为 m ≥3 ．
故结论 ④ 正确．
故选： B ．
【点睛】
本题主要考查了二次函数图象与二次函数的系数的关系，是一道综合性比较强的题目，需要利用数形结合思想解决本题．
4.
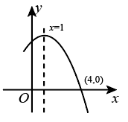
二次函数 的部分图象如图所示，图象过点
，对称轴为
．下列结论： ①
； ②
； ③
； ④
； ⑤ 对于任意实数 m ，式子
都成立．其中结论正确的个数是（ ）
A ． 2 个 B ． 3 个 C ． 4 个 D ． 5 个
难度：
知识点：函数
使用次数：250
【答案】
C
【解析】
【分析】
根据抛物线对称轴为直线 ，可判断 ①③ ，由抛物线开口方向， b = ﹣ 2a ，抛物线与 y 轴交点位置可以判断 ② ，由图象得 x = ﹣ 1 ， y ＜ 0 ，根据抛物线对称性可得 x =3 ， y ＜ 0 ，进而判断 ④ ，由 x =1 时， y 取最大值可判断 ⑤ ．
【详解】
解： ∵ 抛物线对称轴为直线 ，
∴ b = ﹣ 2 a ， ① 正确，符合题意；
∴ ， ③ 正确，符合题意；
∵ x = ﹣ 1 ， y ＜ 0 ，
∴ ，
∵ b = ﹣ 2 a ，
∴15 a + c ＜ 0 ， ② 正确，符合题意；
∵ x = ﹣ 1 ， y = ＜ 0 ，根据抛物线对称性可得 x =3 时， y ＜ 0 ，
∴ ， ④ 正确，符合题意
∵ x =1 时， y 取最大值，
∴ ，
∴ ， ⑤ 错误，不符合题意．
故选： C ．
【点睛】
本题考查二次函数图象与系数的关系，解题关键是掌握二次函数的性质，掌握二次函数与方程及不等式的关系．
5.
已知关于 x 的方程 的两个根分别是 -1 和 3 ，若抛物线
与 y 轴交于点 A ，过 A 作
轴，交抛物线于另一交点 B ，则 AB 的长为（ ）
A ． 2 B ． 3 C ． 1 D ． 1.5
难度：
知识点：二次函数与一元二次方程
使用次数：100
【答案】
A
【解析】
【分析】
根据方程的两根求出 b 、 c 的值，代入抛物线解析式，求出点 A 坐标， A 、 B 两点纵坐标相同，从而求出 B 点坐标， AB 的长即可求出．
【详解】
将 -1 ， 3 分别代入 ，
，
解得 ，
∴ 抛物线解析式为： ，
∴ 与 y 轴交点为： A （ 0 ， 6 ），
∵ AB ⊥ y 轴， ∴ B 的纵坐标为 6 ，
代入抛物线解得， ，
∴ B （ 2 ， 6 ）
∴ AB =2-0=2 ．
故选： A ．
【点睛】
本题考查了抛物线与 y 轴的交点，根与系数的关系，二次函数图象上点的坐标特征，掌握根与系数的关系是解题的关键．
本卷还有25题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
30
总体难度：
中等
难度统计
难度系数
数量
占比
基础
4
13.33%
容易
12
40.0%
中等
14
46.66%
题型统计
大题类型
数量
占比
选择题
20
66.66%
填空题
10
33.33%
知识点统计
知识点
数量
占比
函数
5
16.66%
二次函数的图象和性质
17
56.66%
二次函数与一元二次方程
5
16.66%
二次根式
1
3.33%
解一元二次方程
1
3.33%
一次函数
1
3.33%
版权提示
该作品由: 用户fpy分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。