下列各数: ,
, 0 ,
,其中比
小的数是( )
A . B .
C . 0 D .
A
【分析】
根据正数比负数大,正数比 0 大,负数比 0 小,两个负数中,绝对值大的反而小解答即可.
【详解】
解: ∵∣ ﹣ 4∣=4 , 4 > 3 > 2.8 ,
∴ ﹣ 4 <﹣ 3 <﹣ 2.8 < 0 < ∣ ﹣ 4∣ ,
∴ 比﹣ 3 小的数为﹣ 4 ,
故选: A .
【点睛】
本题考查有理数大小比较,熟知有理数的比较大小的法则是解答的关键.
下列运算正确的是( )
A . B .
C . D .
D
【分析】
分别根据合并同类项法则、积的乘方运算法则、完全平方公式、平方差公式进行判断即可.
【详解】
解: A 、 x 2 和 x 3 不是同类项,不能合并,此选项错误;
B 、 ,此选项错误;
C 、 ,此选项错误;
D 、 ,此选项正确,
故选: D .
【点睛】
本题考查了同类项、积的乘方、完全平方公式、平方差公式,熟记公式,掌握运算法则是解答的关键.
如图是由若干个同样大小的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图是( )
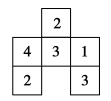
A . 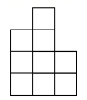 B .
B . 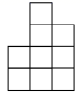 C .
C . 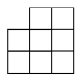 D .
D . 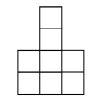
B
【分析】
直接从左边观察几何体,确定每列最高的小正方体个数,即对应左视图的每列小正方形的个数,即可确定左视图.
【详解】
解:如图所示:从左边看几何体,第一列是 2 个正方体,第二列是 4 个正方体,第三列是 3 个正方体;因此得到的左视图的小正方形个数依次应为 2,4,3 ;
故选: B .
【点睛】
本题考查了几何体的三视图,要求学生理解几何体的三种视图并能明白左视图的含义,能确定几何体左视图的形状等,解决本题的关键是牢记三视图定义及其特点,能读懂题意和从题干图形中获取必要信息等,本题蕴含了数形结合的思想方法,对学生的空间想象能力有一定的要求.
如图,直线 ,三角尺的直角顶点在直线 m 上,且三角尺的直角被直线 m 平分,若
,则下列结论错误的是( )
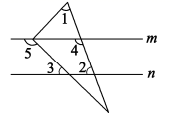
A . B .
C .
D .
D
【分析】
根据角平分线的定义求出 ∠6 和 ∠7 的度数,再利用平行线的性质以及三角形内角和求出 ∠3 , ∠8 , ∠2 的度数,最后利用邻补角互补求出 ∠4 和 ∠5 的度数.
【详解】
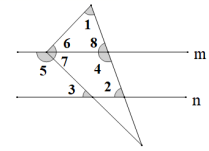
首先根据三角尺的直角被直线 m 平分,
∴∠6=∠7=45° ;
A 、 ∵∠1=60° , ∠6=45° , ∴∠8=180°-∠1-∠6=180-60°-45°=75° , m∥n , ∴∠2=∠8=75° 结论正确,选项不合题意;
B 、 ∵∠7=45° , m ∥ n , ∴∠3=∠7=45° ,结论正确,选项不合题意;
C 、 ∵∠8=75° , ∴∠4=180-∠8=180-75°=105° ,结论正确,选项不合题意;
D 、 ∵∠7=45° , ∴∠5=180-∠7=180-45°=135° ,结论错误,选项符合题意.
故选: D .
【点睛】
本题考查了角平分线的定义,平行线的性质,三角形内角和,邻补角互补,解答本题的关键是掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补.
为了落实 “ 作业、睡眠、手机、读物、体质 ” 等五项管理要求,了解学生的睡眠状况,调查了一个班 50 名学生每天的睡眠时间,绘成睡眠时间频数分布直方图如图所示,则所调查学生睡眠时间的众数,中位数分别为( )
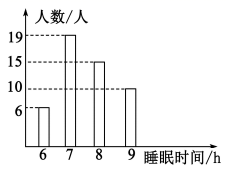
A . 7 h ; 7 h B . 8 h ; 7.5 h C . 7 h ; 7.5 h D . 8 h ; 8 h
C
【分析】
根据众数的定义及所给频数分布直方图可知,睡眠时间为 7 小时的人数最多,根据中位数的定义,把睡眠时间按从小到大排列,第 25 和 26 位学生的睡眠时间的平均数是中位数,从而可得结果.
【详解】
由频数分布直方图知,睡眠时间为 7 小时的人数最多,从而众数为 7h ;
把睡眠时间按从小到大排列,第 25 和 26 位学生的睡眠时间的平均数是中位数,
而第 25 位学生的睡眠时间为 7h ,第 26 位学生的睡眠时间为 8h ,其平均数为 7.5h ,
故选: C .
【点睛】
本题考查了频数分布直方图,众数和中位数,读懂频数分布直方图,掌握众数和中位数的定义是解决本题的关键.
本卷还有20题,登录并加入会员即可免费使用哦~

该作品由: 用户小小分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。