初中数学2021年初专题周练——平行线及其判定训练题（一）【含详解】
初中
整体难度：中等
2021-03-24
题号
一
二
三
四
五
评分
一、选择题 (共46题)
添加该题型下试题
1.
如图，下列能判定 AB ∥ EF 的条件有 ( )
①∠ B ＋ ∠ BFE ＝ 180° ； ②∠ 1 ＝ ∠ 2 ； ③∠ 3 ＝ ∠ 4 ； ④∠ B ＝ ∠ 5.
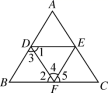
A ． 1 个 B ． 2 个 C ． 3 个 D ． 4 个
难度：
知识点：平行线及其判定
使用次数：108
【答案】
C
【详解】
试题分析：根据平行线的判定定理分别进行判断即可．
解：当 ∠ B+ ∠ BFE=180° ， AB ∥ EF ；当 ∠ 1= ∠ 2 时， DE ∥ BC ；当 ∠ 3= ∠ 4 时， AB ∥ EF ；当 ∠ B= ∠ 5 时， AB ∥ EF ．
故选 C ．
考点：平行线的判定．
2.
如图，直线 a，b 被直线 c 所截，下列条件中，不能判定 a ∥ b（ ）
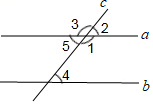
A ． ∠ 2= ∠ 4 B ． ∠ 1+ ∠ 4=180° C ． ∠ 5= ∠ 4 D ． ∠ 1= ∠ 3
难度：
知识点：平行线及其判定
使用次数：248
【答案】
D
【解析】 根据同位角相等，两直线平行；同旁内角互补，两直线平行；内错角相等，两直线平行，进行判断即可．
【详解】由 ∠ 2= ∠ 4 或 ∠ 1+ ∠ 4=180° 或 ∠ 5= ∠ 4 ，可得 a ∥ b；
由 ∠ 1= ∠ 3 ，不能得到 a ∥ b，
故选 D．
【点睛】本题主要考查了平行线的判定，熟记平行线的判定方法是解题的关键 . 解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．本题是一道探索性条件开放型题目，能有效地培养 “ 执果索因 ” 的思维方式与能力．
3.
如图，给出了过直线外一点作已知直线的平行线的方法，其依据是 ( )
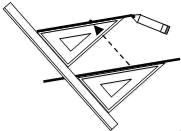
A ． 同位角相等，两直线平行 B ． 内错角相等，两直线平行
C ． 同旁内角互补，两直线平行 D ． 两直线平行，同位角相等
难度：
知识点：平行线及其判定
使用次数：193
【答案】
A
【解析】
试题分析：判定两条直线是平行线的方法有：内错角相等，两直线平行；同位角相等，两直线平行；同旁内角互补两直线平行等，应结合题意，具体情况，具体分析．
由图形得，有两个相等的同位角，所以只能依据：同位角相等，两直线平行，
故选 A.
考点：本题考查的是平行线的判定
点评：正确识别 “ 三线八角 ” 中的同位角、内错角、同旁内角是正确答题的关键，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
4.
如下图，下列条件中： ①∠ B+ ∠ BCD=180° ； ②∠1=∠2；③∠3=∠4；④∠ B= ∠5，能判定 AB ∥ CD 的条件为（ ）
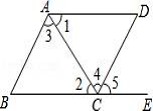
A ． ①②③④ B ． ①②④ C ． ①③④ D ． ①②③
难度：
知识点：平行线及其判定
使用次数：256
【答案】
C
【详解】
解： ①∵∠ B+ ∠ BCD=180 °，
∴ AB ∥ CD ；
②∵∠ 1= ∠ 2 ，
∴ AD ∥ BC ；
③∵∠ 3= ∠ 4 ，
∴ AB ∥ CD ；
④∵∠ B= ∠ 5 ，
∴ AB ∥ CD ；
∴能得到 AB ∥ CD 的条件是 ①③④．
故选 C ．
【点睛】
此题主要考查了平行线的判定，解题关键是合理利用平行线的判定，确定同位角、内错角、同旁内角 . 平行线的判定：同旁内角互补，两直线平行；内错角相等，两直线平行；
同位角相等，两直线平行 .
5.
在同一平面内，设 a、b、c 是三条互相平行的直线，已知 a 与 b 的距离为 4cm，b 与 c 的距离为 1cm ，则 a 与 c 的距离为（ ）
A ． 1cm B ． 3cm C ． 5cm 或 3cm D ． 1cm 或 3cm
难度：
知识点：相交线
使用次数：243
【答案】
C
【解析】
分析：分类讨论：当直线 c 在 a、b 之间或直线 c 不在 a、b 之间，然后利用平行线间的距离的意义分别求解．
详解：当直线 c 在 a、b 之间时，
∵ a、b、c 是三条平行直线，
而 a 与 b 的距离为 4cm，b 与 c 的距离为 1cm，
∴ a 与 c 的距离 =4-1=3（cm）；
当直线 c 不在 a、b 之间时，
∵ a、b、c 是三条平行直线，
而 a 与 b 的距离为 4cm，b 与 c 的距离为 1cm，
∴ a 与 c 的距离 =4+1=5（cm），
综上所述， a 与 c 的距离为 3cm 或 5cm．
故选 C．
点睛：本题考查了平行线之间的距离，从一条平行线上的任意一点到另一条直线作垂线，垂线段的长度叫两条平行线之间的距离．平行线间的距离处处相等．注意分类讨论．
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
中等
难度统计
难度系数
数量
占比
中等
55
55.00%
基础
10
10.0%
偏难
13
13.0%
很难
3
3.0%
容易
19
19.0%
题型统计
大题类型
数量
占比
选择题
46
46.0%
解答题
40
40.0%
填空题
14
14.00%
知识点统计
知识点
数量
占比
平行线及其判定
88
88.0%
相交线
5
5.0%
角
6
6.0%
三角形全等的判定
1
1.0%
版权提示
该作品由: 用户我爱真理分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。