2012山东人教版初中数学中考真题45713
初中
整体难度：中等
2012-07-05
题号
一
二
三
四
五
评分
一、选择题 (共10题)
添加该题型下试题
1.
在数轴上到原点距离等于2的点所标示的数是（ ）
|
| A． | ﹣2 | B． | 2 | C． | ±2 | D． | 不能确定 |
难度：
知识点：有理数
使用次数：141
【答案】
考点： 数轴。
分析： 先在数轴上标出到原点距离等于2的点，然后根据图示作出选择即可．
解答： 解：在数轴上到原点距离等于2的点如图所示：
点A、B即为所求的点，即在数轴上到原点距离等于2的点所标示的数是﹣2和2；
故选C．
点评： 本题考查了数轴．由于引进了数轴，我们把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想．
2.
下列运算正确的是（ ）
|
| A． | ﹣2（3x﹣1）=﹣6x﹣1 | B． | ﹣2（3x﹣1）=﹣6x+1 | C． | ﹣2（3x﹣1）=﹣6x﹣2 | D． | ﹣2（3x﹣1）=﹣6x+2 |
难度：
知识点：整式的乘法
使用次数：134
【答案】
考点：
去括号与添括号。
分析：
利用去括号法则，将原式去括号，进而判断即可得出答案即可．
解答：
解：A．∵﹣2（3x﹣1）=﹣6x+2，∴﹣2（3x﹣1）=﹣6x﹣1错误，故此选项错误；
B．∵﹣2（3x﹣1）=﹣6x+2，∴﹣2（3x﹣1）=﹣6x+1错误，故此选项错误；
C．∵﹣2（3x﹣1）=﹣6x+2，∴﹣2（3x﹣1）=﹣6x﹣2错误，故此选项错误；
D．﹣2（3x﹣1）=﹣6x+2，故此选项正确；
故选：D．
点评：
此题主要考查了去括号法则，利用去括号法则：如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反得出是解题关键．
3.
空气是由多种气体混合而成的，为了简明扼要的介绍空气的组成情况，较好的描述数据，最适合使用的统计图是（ ）
|
| A． | 扇形图 | B． | 条形图 | C． | 折线图 | D． | 直方图 |
难度：
知识点：统计调查
使用次数：153
【答案】
考点：
统计图的选择。
分析：
扇形统计图表示的是部分在总体中所占的百分比，但一般不能直接从图中得到具体的数据；
折线统计图表示的是事物的变化情况；
条形统计图能清楚地表示出每个项目的具体数目；
频数分布直方图，清楚显示在各个不同区间内取值，各组频数分布情况，易于显示各组之间频数的差别．
解答：
解：根据题意，得
要求直观反映空气的组成情况，即各部分在总体中所占的百分比，结合统计图各自的特点，应选择扇形统计图．
故选A．
点评：
此题考查扇形统计图、折线统计图、条形统计图各自的特点．
4.
下列式子变形是因式分解的是（ ）
|
| A． | x2﹣5x+6=x（x﹣5）+6 | B． | x2﹣5x+6=（x﹣2）（x﹣3） | C． | （x﹣2）（x﹣3）=x2﹣5x+6 | D． | x2﹣5x+6=（x+2）（x+3） |
难度：
知识点：因式分解
使用次数：57
【答案】
考点：
因式分解的意义。
分析：
根据因式分解的定义：就是把整式变形成整式的积的形式，即可作出判断．
解答：
解：A、x2﹣5x+6=x（x﹣5）+6右边不是整式积的形式，故不是分解因式，故本选项错误；
B、x2﹣5x+6=（x﹣2）（x﹣3）是整式积的形式，故是分解因式，故本选项正确；
C、（x﹣2）（x﹣3）=x2﹣5x+6是整式的乘法，故不是分解因式，故本选项错误；
D、x2﹣5x+6=（x﹣2）（x﹣3），故本选项错误．
故选B．
点评：
本题考查的是因式分解的意义，把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，也叫做分解因式．
5.
用直尺和圆规作一个角的平分线的示意图如图所示，则能说明∠AOC=∠BOC的依据是（ ）
|
| A． | SSS | B． | ASA |
|
| C． | AAS | D． | 角平分线上的点到角两边距离相等 |
难度：
知识点：三角形全等的判定
使用次数：172
【答案】
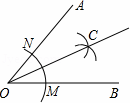
考点：
全等三角形的判定与性质；作图—基本作图。
专题：
证明题。
分析：
连接NC，MC，根据SSS证△ONC≌△OMC，即可推出答案．
解答：
解：连接NC，MC，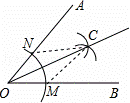
在△ONC和△OMC中
，
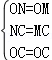∴△ONC≌△OMC（SSS），
∴∠AOC=∠BOC，
故选A．
点评：
本题考查了全等三角形的性质和判定的应，主要考查学生运用性质进行推理的能力，题型较好，难度适中．
本卷还有18题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
23
总体难度：
中等
难度统计
难度系数
数量
占比
容易
11
47.82%
中等
11
47.82%
偏难
1
4.34%
题型统计
大题类型
数量
占比
选择题
10
43.47%
填空题
4
17.39%
解答题
7
30.43%
计算题
1
4.34%
综合题
1
4.34%
知识点统计
知识点
数量
占比
有理数
1
4.34%
整式的乘法
1
4.34%
统计调查
2
8.69%
因式分解
1
4.34%
三角形全等的判定
1
4.34%
一次函数
2
8.69%
角
1
4.34%
勾股定理
1
4.34%
几何图形
1
4.34%
特殊的平行四边形
2
8.69%
整式
1
4.34%
锐角三角函数
2
8.69%
反比例函数
1
4.34%
一元一次不等式组
1
4.34%
实际问题与一元二次方程
1
4.34%
点和圆、直线和圆的位置关系
1
4.34%
中心对称
1
4.34%
用列举法求概率
1
4.34%
各地中考
1
4.34%
版权提示
该作品由: 用户ewwerf分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。