如图，是底部B

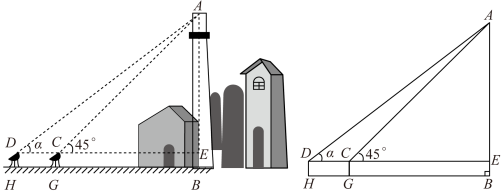
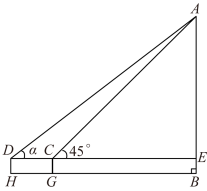
如图，是底部 B 不可到达的一座建筑物， A 为建筑物的最高点，测角仪器的高米．某数学兴趣小组为测量建筑物的高度，先在 H 处用测角仪器测得建筑物顶端 A 处的仰角为，再向前走 5 米到达 G 处，又测得建筑物顶端 A 处的仰角为，已知， H ， G ， B 三点在同一水平线上，求建筑物的高度．

答案

19 米

【分析】设米．在中，得到．在中，得到，．根据，列方程．

【详解】解：如图．根据题意，，

．

设米．在中，

∵ ，

∴ ．

在中， ∵ ，

∴ ．

∵ ，

∴ ，

∴ （经检验符合实际），即．

∵ ，

∴ （米）．

答：建筑物的高度为 19 米．

【点睛】本题考查了解三角形的应用问题，锐角三角函数的应用，解题的关键是找出直角三角形，熟练利用正切函数的定理求解．

当前位置：

学科首页

八上第十三章轴对称

等腰三角形

试题详情

难度：

使用次数：180

更新时间：2023-04-16

纠错

查看答案

题型：解答题

知识点：等腰三角形

下载试题

复制试题

【答案】

19 米

【分析】设米．在中，得到．在中，得到，．根据，列方程．

【详解】解：如图．根据题意，，

．

设米．在中，

∵ ，

∴ ．

在中， ∵ ，

∴ ．

∵ ，

∴ ，

∴ （经检验符合实际），即．

∵ ，

∴ （米）．

答：建筑物的高度为 19 米．

【点睛】本题考查了解三角形的应用问题，锐角三角函数的应用，解题的关键是找出直角三角形，熟练利用正切函数的定理求解．

考点梳理:

根据可圈可点权威老师分析，试题“ ”主要考查你对等腰三角形的性质，等腰三角形的判定等考点的理解。关于这些考点的“资料梳理”如下：

◎ 等腰三角形的性质，等腰三角形的判定的定义

定义：
有两条边相等的三角形，是等腰三角形，相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。

◎ 等腰三角形的性质，等腰三角形的判定的知识扩展

1、定义：有两条边相等的三角形，是等腰三角形，相等的两条边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。
2、性质：（1）等腰三角形的两个底角相等（简称：等边对等角）；
（2）等腰三角形顶角平分线平分底边并且垂直于底边。即等腰三角形的顶角平分线、底边上的中线、底边上的高重合。
3、判定：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）。这个判定定理常用于证明同一个三角形中的边相等。

◎ 等腰三角形的性质，等腰三角形的判定的特性

等腰三角形的性质：
1.等腰三角形的两个底角度数相等（简写成“等边对等角”）。
2.等腰三角形的顶角的平分线，底边上的中线，底边上的高重合（简写成“等腰三角形的三线合一”）。
3.等腰三角形的两底角的平分线相等（两条腰上的中线相等，两条腰上的高相等）。
4.等腰三角形底边上的垂直平分线到两条腰的距离相等。
5.等腰三角形的一腰上的高与底边的夹角等于顶角的一半。
6.等腰三角形底边上任意一点到两腰距离之和等于一腰上的高（需用等面积法证明）。
7.等腰三角形是轴对称图形，只有一条对称轴，顶角平分线所在的直线是它的对称轴，等边三角形有三条对称轴。
8.等腰三角形中腰的平方等于高的平方加底的一半的平方
9.等腰三角形中腰大于高
10.等腰三角形底边延长线上任意一点到两腰距离之差等于一腰上的高(需用等面积法证明)

◎ 等腰三角形的性质，等腰三角形的判定的知识点拨

等腰三角形的判定：
1.定义法：在同一三角形中，有两条边相等的三角形是等腰三角形。
2.判定定理：在同一三角形中，有两个角相等的三角形是等腰三角形（简称：等角对等边）。
3.顶角的平分线，底边上的中分线，底边上的高的重合的三角形是等腰三角形。

◎ 等腰三角形的性质，等腰三角形的判定的教学目标

1、理解等腰三角形的性质和判定方法。
2、会运用等腰三角形的性质和判定进行有关的计算与简单的证明。
3、学会文字命题的证明方法、基本步骤和书写格式。
4、逐步学会分析几何证明题的方法及用规范的数学语言表述证明过程。

◎ 等腰三角形的性质，等腰三角形的判定的考试要求

能力要求：掌握
课时要求：70
考试频率：必考
分值比重：4

开通会员

登录并加入会员可无限制查看知识点解析

类题推荐：

等腰三角形

难度：

使用次数：98